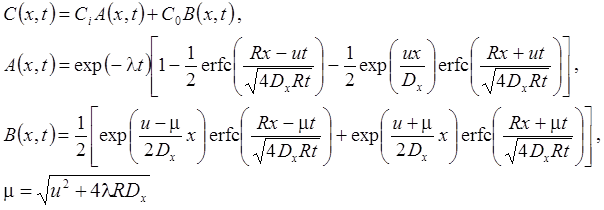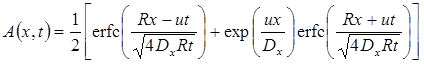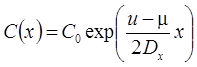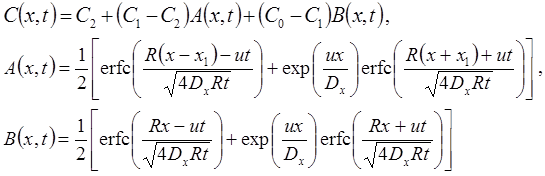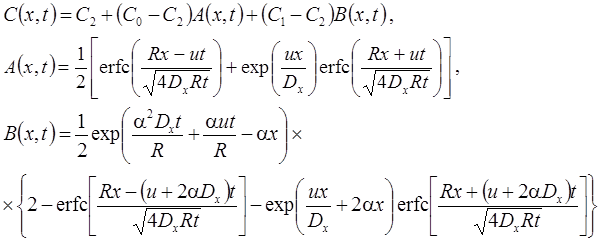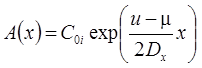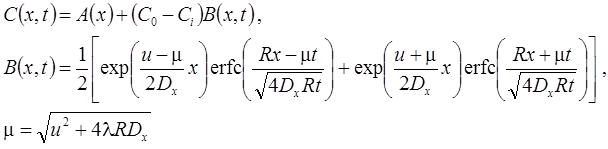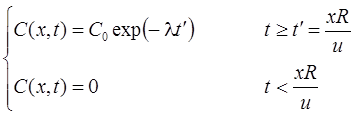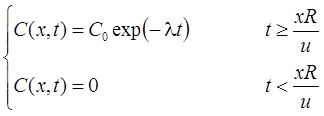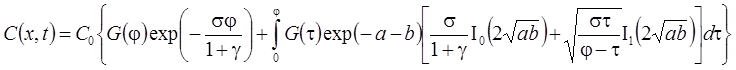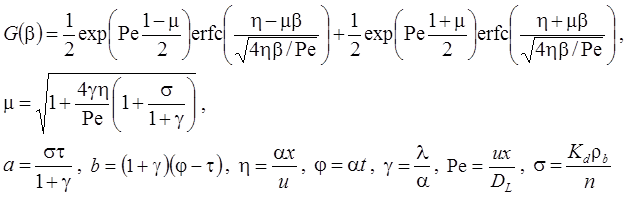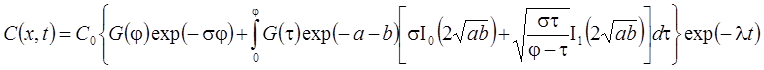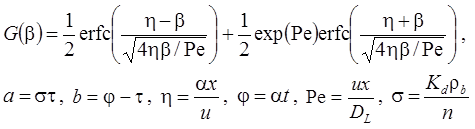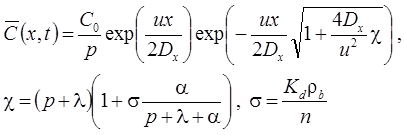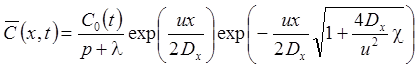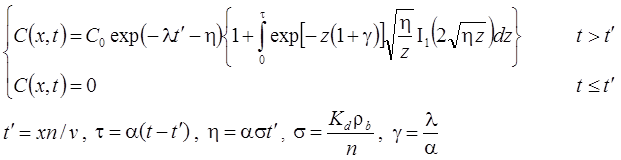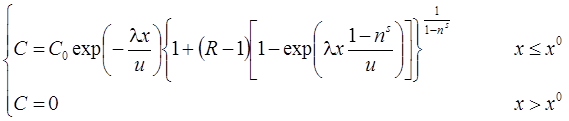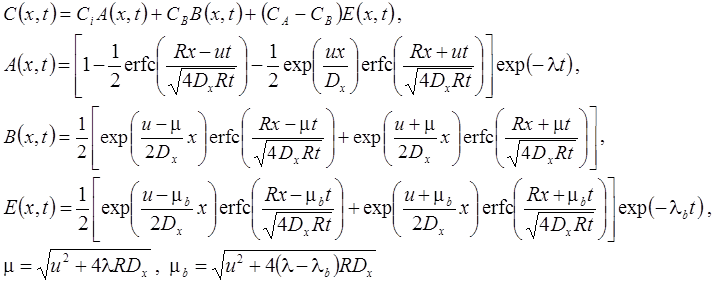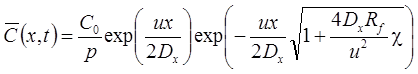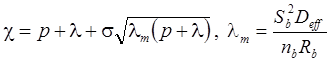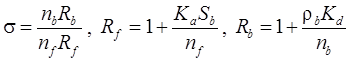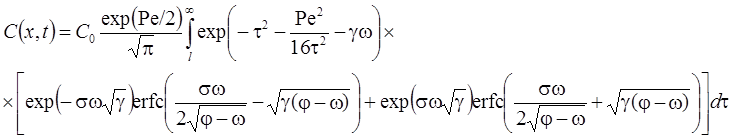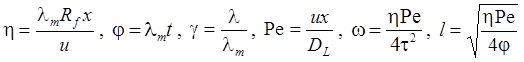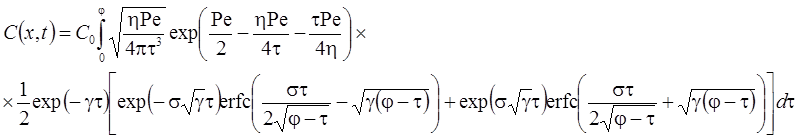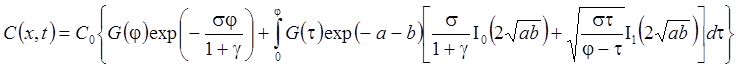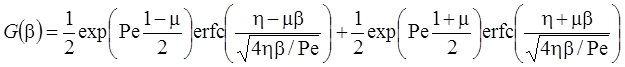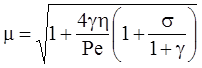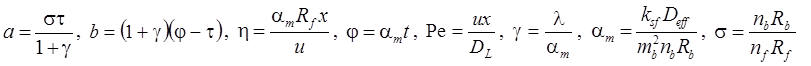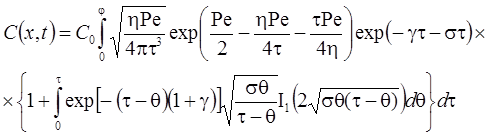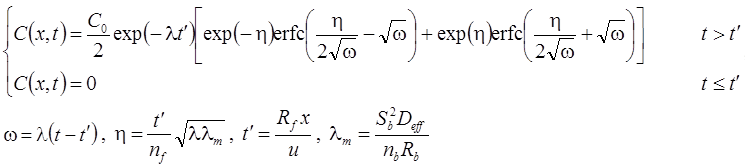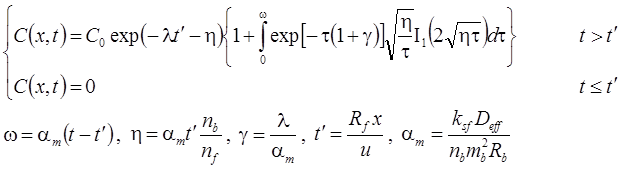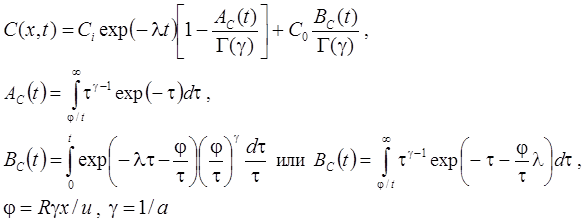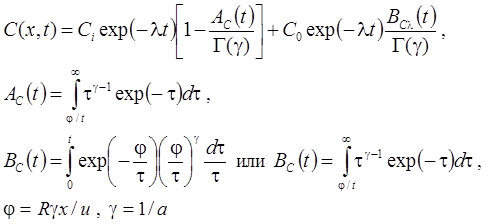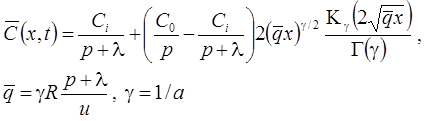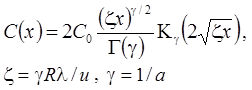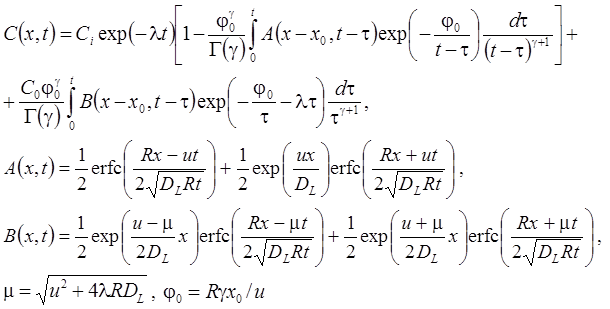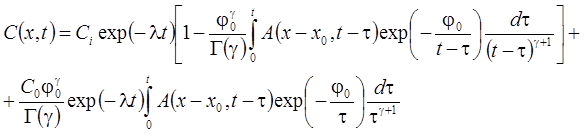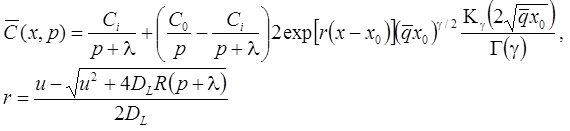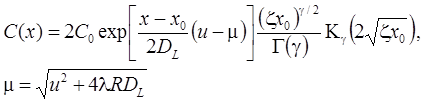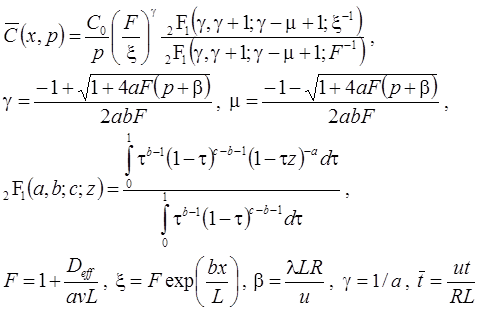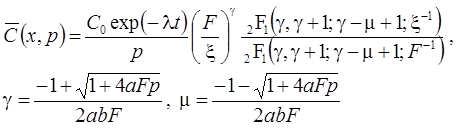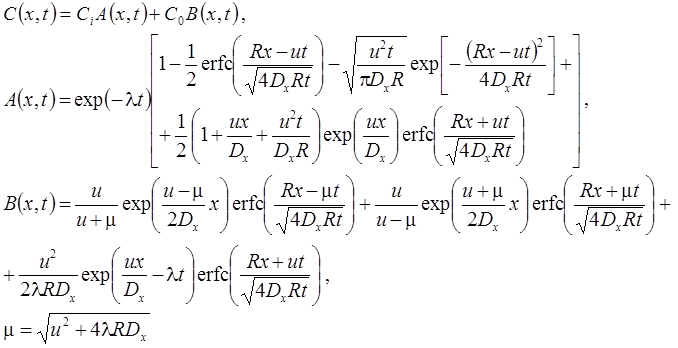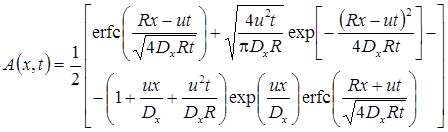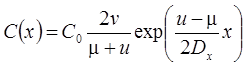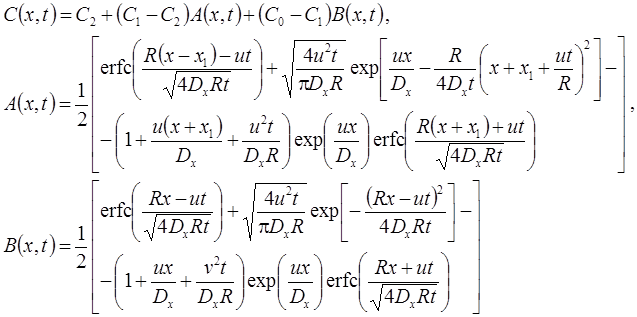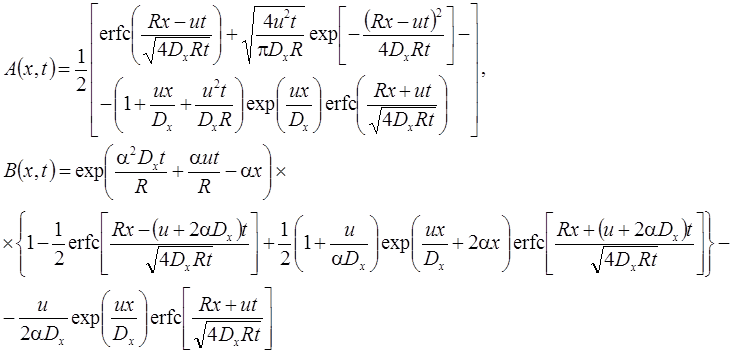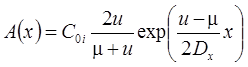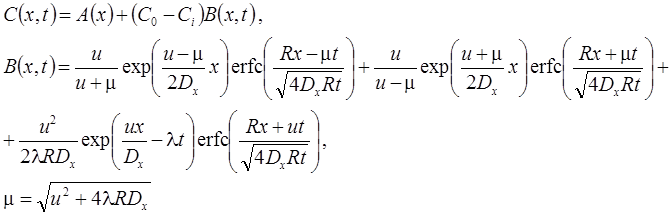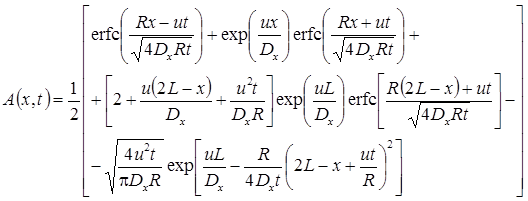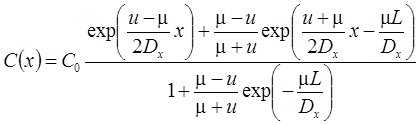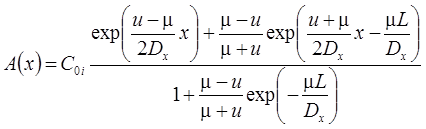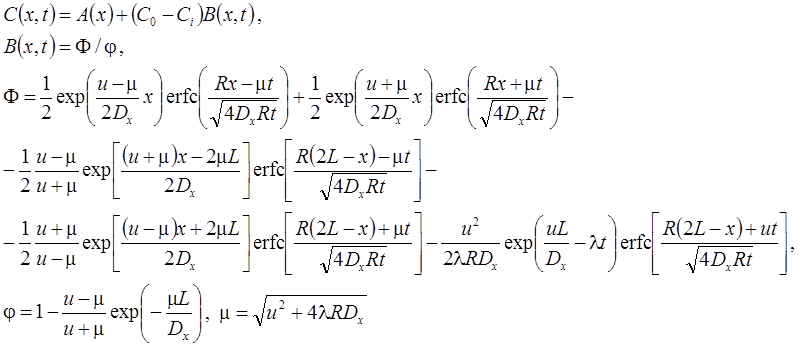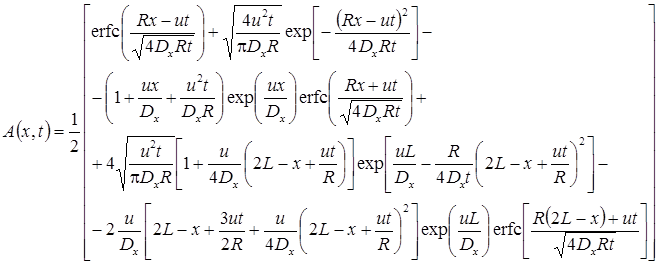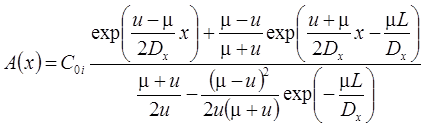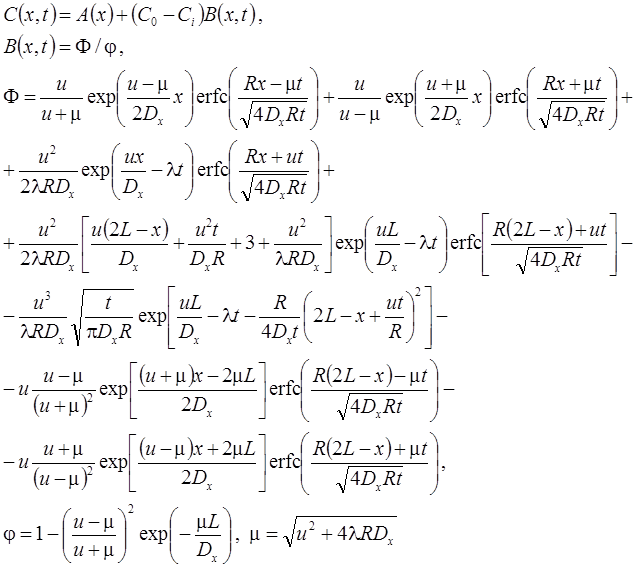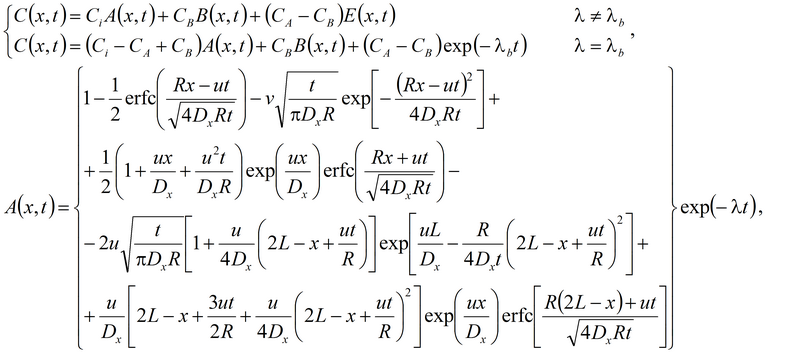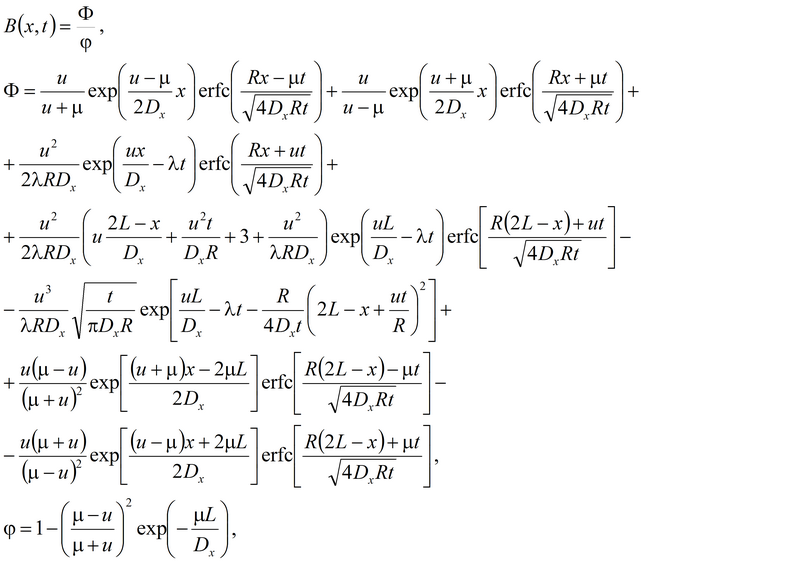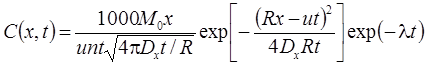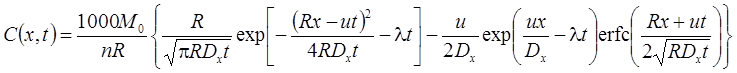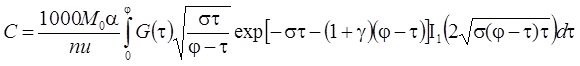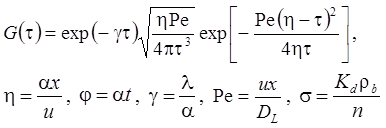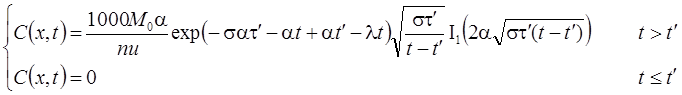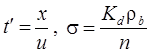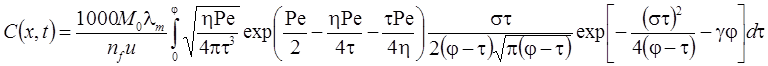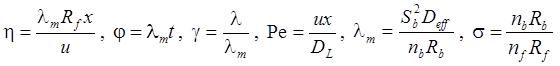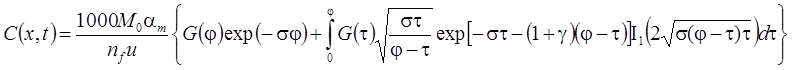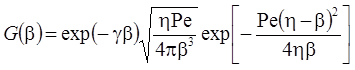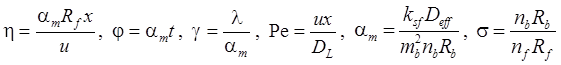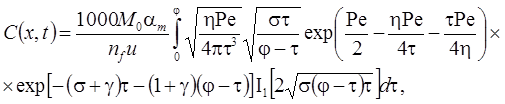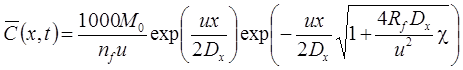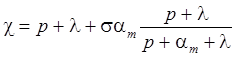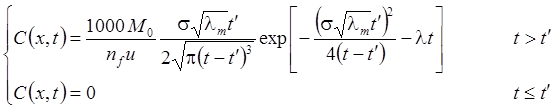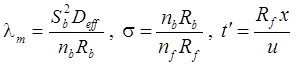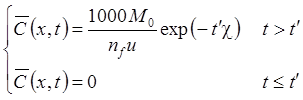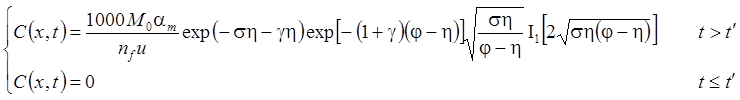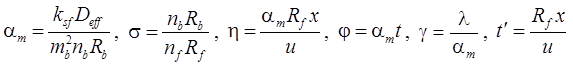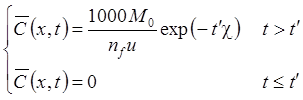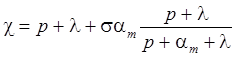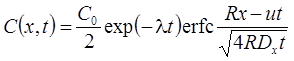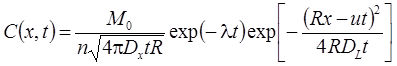Базовые уравнения

Решение миграционных задач > Одномерные задачи >

Базовые уравнения

Приводятся базовые уравнения для расчета миграции в одномерном потоке. На их основе строятся решения для пакетного запуска вещества и упрощенные решения без учета сорбции и распада.

Литература

Van Genuchten M.Th., Alves W.J. Analytical solutions of the one-dimensional convective-dispersive solute transport equations. U.S. department of agriculture, Technical bulletin No. 1661. 1982.

Румынин В.Г. Геомиграционные модели в гидрогеологии. СПб.: Недра, 2011.

Румынин В.Г. Теория и методы изучения загрязнения подземных вод. СПб.: Наука, 2020.

Rumynin V.G. Subsurface solute transport models and case histories. With applications to radionuclide migration. Springer, 2011.

Gutierrez A. et al. TRAC, a collaborative computer tool for tracer-test interpretation. EPJ Web of Conferences 50, 03002. 2013. DOI: 10.1051/epjconf/20135003002.

Tang D.H., Frind E.O., Sudicky E.A. Contaminant transport in fractured porous media: analytical solution for a single fracture // Water Resources Research. 1981. Vol. 17, N 3. P. 555–564.

Toride N., Leu F.J., van Genuchten M.Th. A comprehensive set of analytical solutions for nonequilibrium solute transport with first-order decay and order-zero decay production // Water Resources Research. 1993. Vol. 29, N 7. P. 2167–2182.

Pérez Guerrero J.S., Pontedeiro E.M., van Genuchten M.Th., Skaggs T.H. Analytical solutions of the one-dimensional advection-dispersion solute transport equation subject to time-dependent boundary conditions // Chemical Engineering Journal. 2013. Vol. 221. P. 487–491.

Huang K., Van Genuchten M.T., Zhang R. Exact solutions for one-dimensional transport with asymptotic scale-dependent dispersion. Appl. Math. Modelling. 1996. Vol. 20, P. 298-308.

Pang L., Hunt B. Solutions and verification of a scale-dependent dispersion model. Journal of Contaminant Hydrology. 2001. Vol. 53. P. 21-39.

Yates S.R. An analytical solution for one-dimensional transport in porous medium with an exponential dispersion function. Water Resources Research. 1992. Vol. 28, N 8, P. 2149-2154.

Основные условные обозначения:

1а. Распад в пласте, дисперсия, сорбция, начальная концентрация (Van Genuchten, Alves, 1982, Eq. C5):

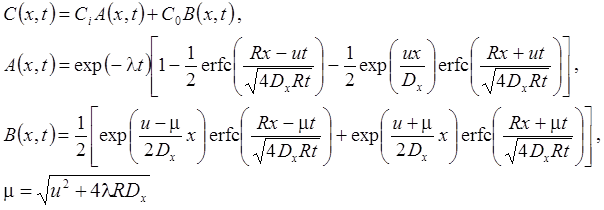
1б. Распад в пласте и на границе, дисперсия, сорбция, начальная концентрация (из Van Genuchten, Alves, 1982, Eq. A1):

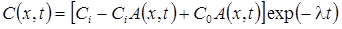
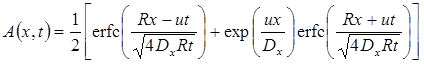
1в. Стационар без распада на границе (Van Genuchten, Alves, 1982, Eq. C1):

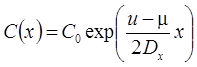
2. Две зоны начальной концентрации C1 (от x = 0 до x = x1) и C2 (от x = x1 до x = ∞): без распада, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A5):

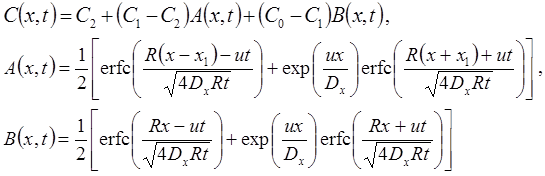
3. Функциональное изменение начальной концентрации: без распада, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A7).

Начальная концентрация в пласте меняется от C1 (x = 0) до C2 (x = ∞) по экспоненциальной зависимости:

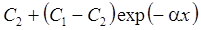
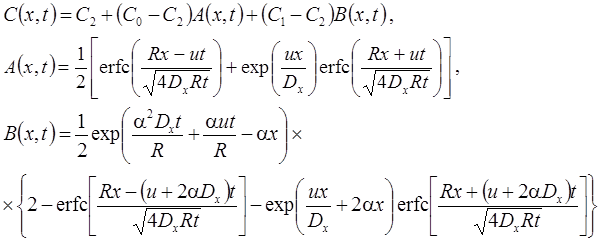
4. Функциональное изменение начальной концентрации: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eqs. C1, C9).

Начальная концентрация в пласте меняется по стационарной зависимости, сформировавшейся при "предыдущем" загрязнении пласта от постоянно действующего источника загрязнения (C0i – константа, определяющая распределение начальной концентрации):

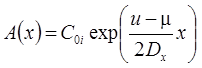
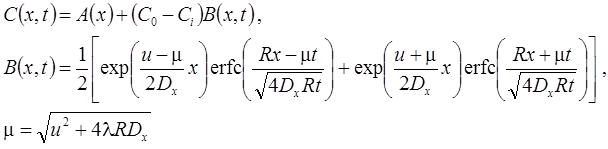
5. Поршневое вытеснение: распад, без дисперсии, сорбция (Румынин, 2020, уравнение 15.4):

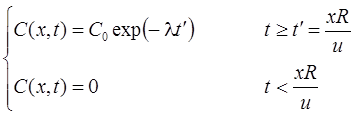
5а. Поршневое вытеснение с учетом распада вещества в растворе на границе: распад, без дисперсии, сорбция (Румынин, 2020, уравнение 15.5а):

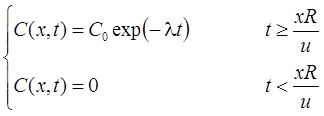
6а. Линейная неравновесная сорбция: распад, дисперсия, сорбция (Toride et al., 1993):

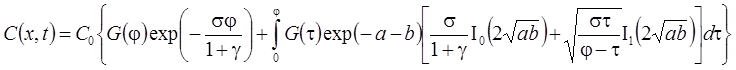
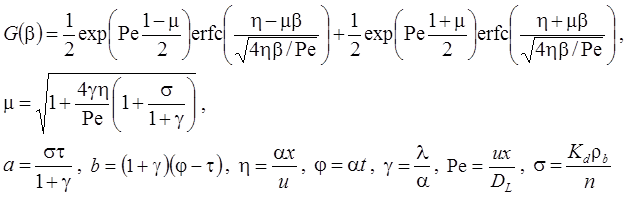
6б. Линейная неравновесная сорбция с учетом распада вещества в растворе на границе: распад, дисперсия, сорбция (Toride et al., 1993):

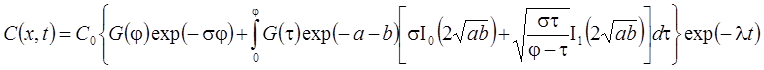
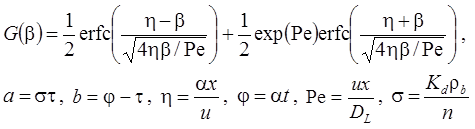
7а. Линейная неравновесная сорбция: распад, дисперсия, сорбция (Rumynin, 2011) – решение задачи в изображениях:

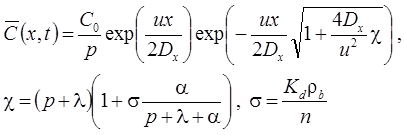
7б. Линейная неравновесная сорбция с учетом распада вещества в растворе на границе: распад, дисперсия, сорбция (Rumynin, 2011) – решение задачи в изображениях:

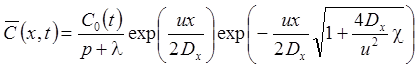
8. Линейная неравновесная сорбция, поршневое вытеснение: распад, без дисперсии, сорбция (Румынин, 2011, уравнение 7.73):

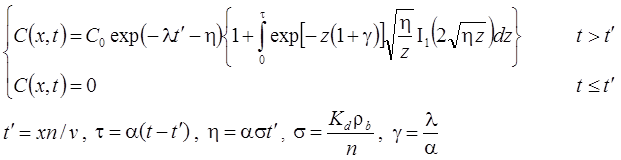
9а. Нелинейная равновесная сорбция (изотерма Френдлиха), поршневое вытеснение: распад, без дисперсии, сорбция (Румынин, 2011, уравнение 17.54):

9б. Стационар (Румынин, 2011, уравнение 17.54):

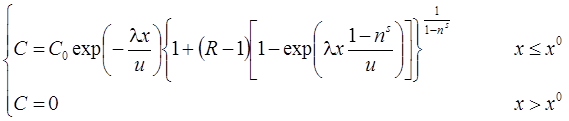
10. Изменение концентрации на границе: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A9).

Граничная концентрация меняется от CA (t = 0) до CB (t = ∞) по экспоненциальной зависимости (λb – константа, характеризующая уменьшение граничной концентрации, 1/сут):

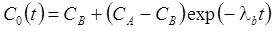
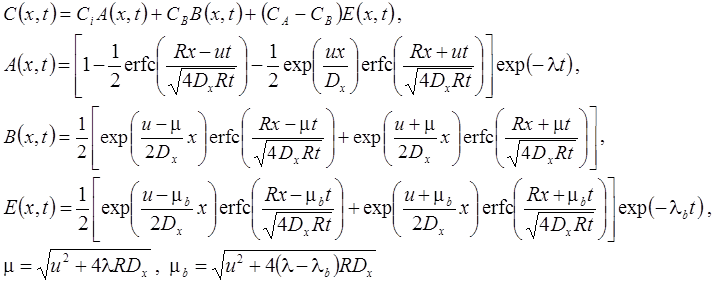
1. Распад, дисперсия, сорбция, начальная концентрация (Rumynin, 2011), решение задачи в изображениях:

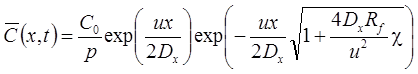
– неограниченная емкость блоков:

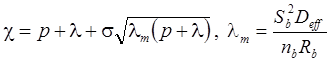
– сосредоточенная емкость блоков:

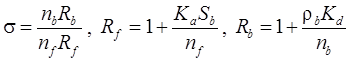
2. Решение функции-оригинала для неограниченной емкости блоков (Tang et al., 1981):

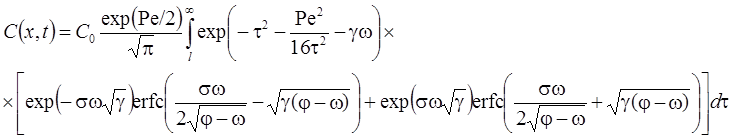
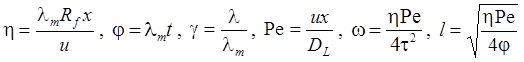
3. Решение функции-оригинала (интеграл свертки) для неограниченной емкости блоков (Rumynin, 2011):

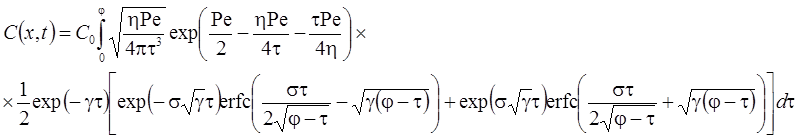
4. Решение функции-оригинала для сосредоточенной емкости блоков (Toride et al., 1993)

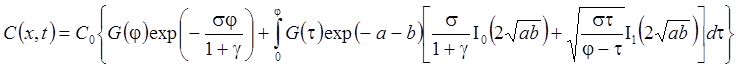
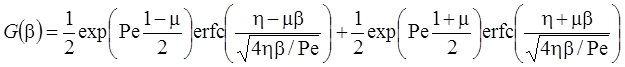
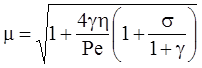
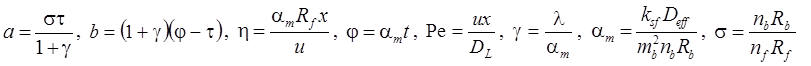
5. Решение функции-оригинала (интеграл свертки) для сосредоточенной емкости блоков (Rumynin, 2011):

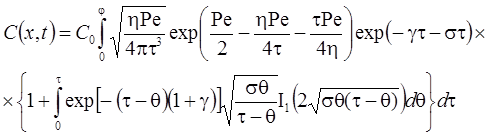
6. Поршневое вытеснение: распад, без дисперсии, сорбция

– неограниченная емкость блоков (Rumynin, 2011, Eq. 6.61):

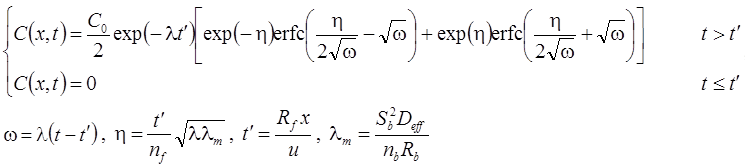
– сосредоточенная емкость блоков (Rumynin, 2011, Eq. 6.64):

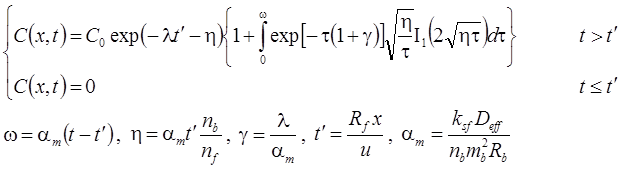
1а. Решение без распада на границе – распад в пласте, сорбция, начальная концентрация (Huang et al., 1996, Eq. 42):

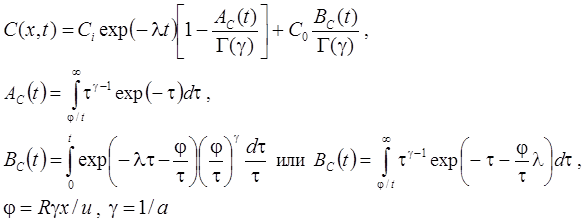
1б. Решение с распадом на границе – распад в пласте, сорбция, начальная концентрация:

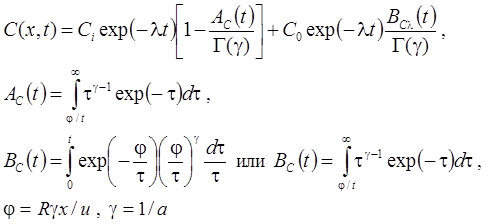
2. Решение без распада на границе (решение задачи в изображениях) – распад в пласте, сорбция, начальная концентрация (Huang et al., 1996, Eq. 39):

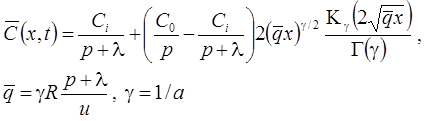
3. Решение стационарной задачи без распада на границе – распад в пласте, сорбция (Huang et al., 1996, Eq. 57):

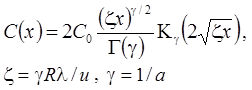
Решения для расстояний меньше или равно x0 см. в аналогичных пунктах для линейной зависимости. Ниже приводятся решения для x > x0.

1а. Решение без распада на границе – распад в пласте, сорбция, начальная концентрация (Huang et al., 1996, Eq. 43):

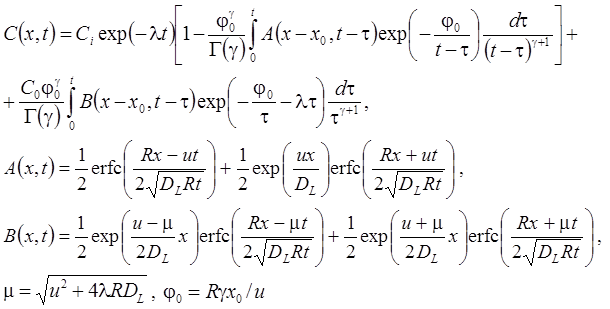
1б. Решение с распадом на границе – распад в пласте, сорбция, начальная концентрация:

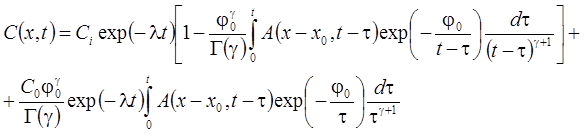
2. Решение без распада на границе (решение задачи в изображениях) – распад в пласте, сорбция, начальная концентрация (Huang et al., 1996, Eq. 40):

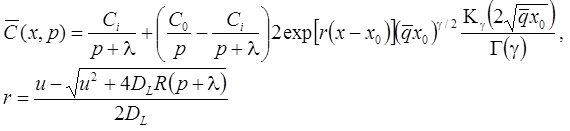
3. Решение стационарной задачи без распада на границе – распад в пласте, сорбция (Huang et al., 1996, Eq. 60):

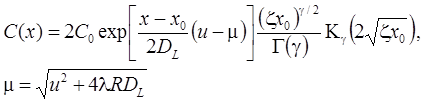
Решение без распада на границе (решение задачи в изображениях) – распад в пласте, сорбция (Yates, 1992, Eq. 12):

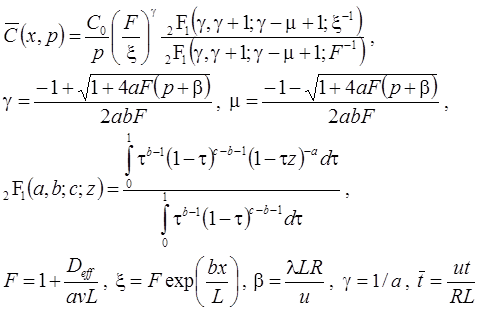
Решение с распадом на границе (решение задачи в изображениях) – распад в пласте, сорбция:

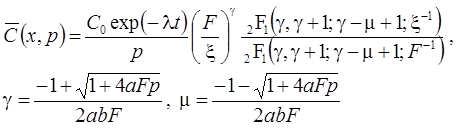
1а. Распад в пласте, дисперсия, сорбция, начальная концентрация (Van Genuchten, Alves, 1982, Eq. C6)

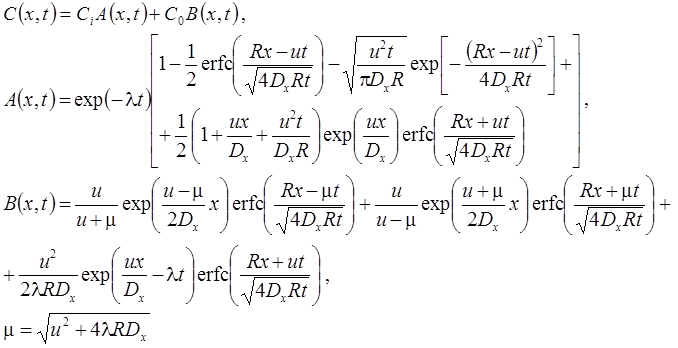
1б. Распад в пласте и на границе, дисперсия, сорбция, начальная концентрация (из Van Genuchten, Alves, 1982, Eq. A2)

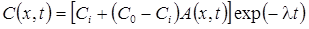
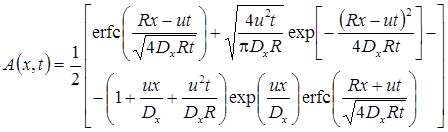
1в. Стационар без распада на границе (Van Genuchten, Alves, 1982, Eq. C2):

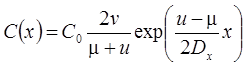
2. Две зоны начальной концентрации C1 (от x = 0 до x = x1) и C2 (от x = x1 до x = ∞): без распада, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A6):

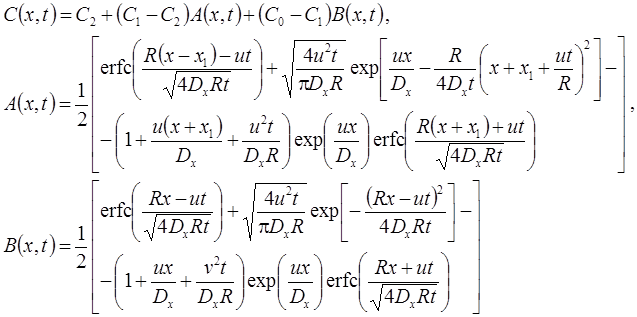
3. Функциональное изменение начальной концентрации: без распада, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A8).

Начальная концентрация в пласте меняется от C1 (x = 0) до C2 (x = ∞) по экспоненциальной зависимости:

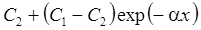
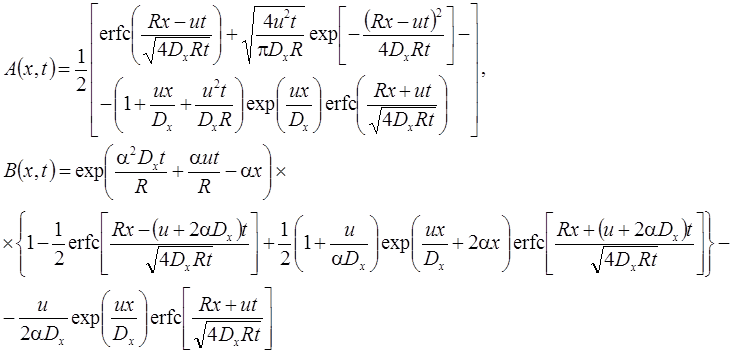
4. Функциональное изменение начальной концентрации: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eqs. C2, C10).

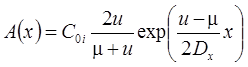
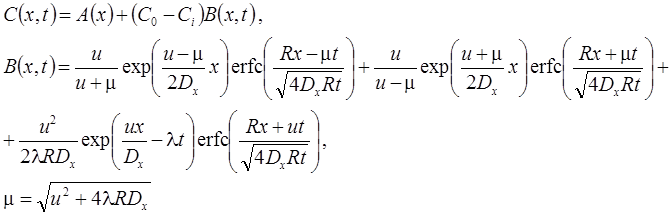
5. Изменение концентрации на границе: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A9).

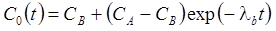
1а. Постоянная концентрация на левой границе: распад в пласте, дисперсия, сорбция, начальная концентрация (Van Genuchten, Alves, 1982, Eq. C7):

1б. Постоянная концентрация на левой границе: распад в пласте и на границе, дисперсия, сорбция, начальная концентрация (из Van Genuchten, Alves, 1982, Eq. A3):

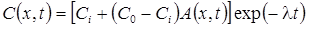
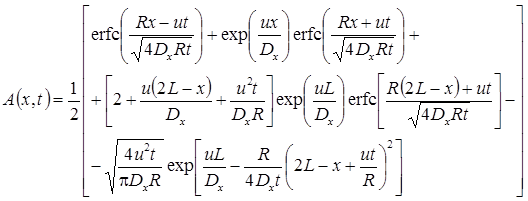
1в. Стационар без распада на границе (Van Genuchten, Alves, 1982, Eq. C3)

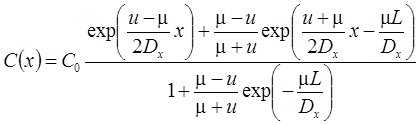
2. Постоянная концентрация на левой границе. Функциональное изменение начальной концентрации: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eqs. C3, C11).

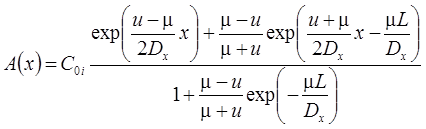
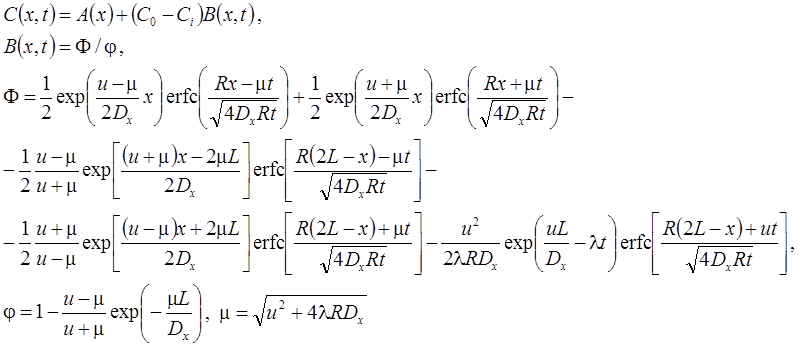
3а. Поток концентрации на левой границе: распад в пласте, дисперсия, сорбция, начальная концентрация (Van Genuchten, Alves, 1982, Eq. C8):

3б. Поток концентрации на левой границе: распад в пласте и на границе, дисперсия, сорбция, начальная концентрация (Van Genuchten, Alves, 1982, Eq. C8):

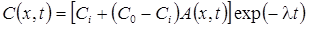
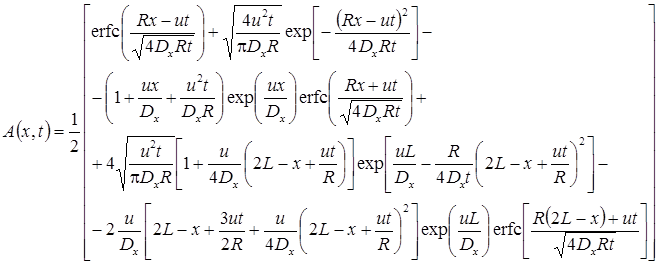
4. Поток концентрации на левой границе. Функциональное изменение начальной концентрации: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eqs. C4, C12).

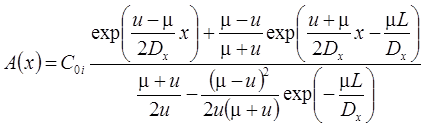
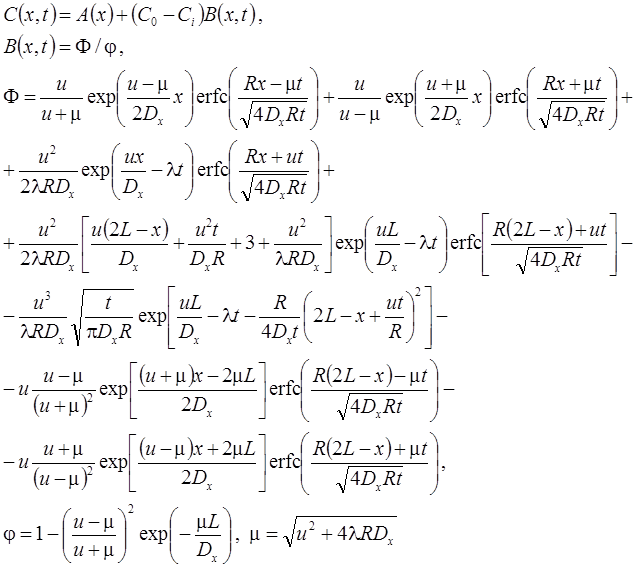
5. I род + изменение концентрации на границе: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A11).

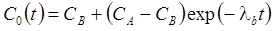
6. Поток + изменение концентрации на границе: распад, дисперсия, сорбция (Van Genuchten, Alves, 1982, Eq. A12).

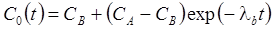
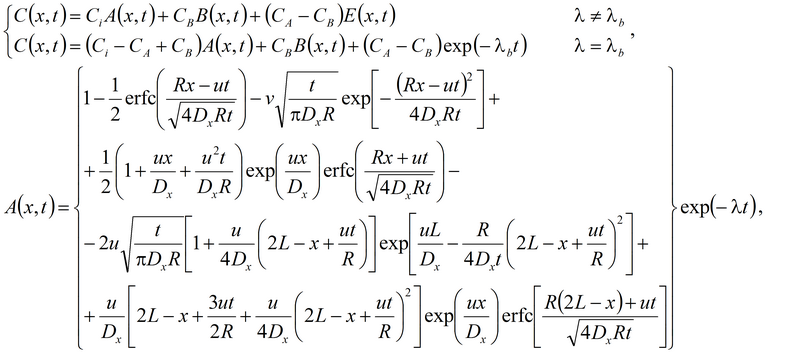
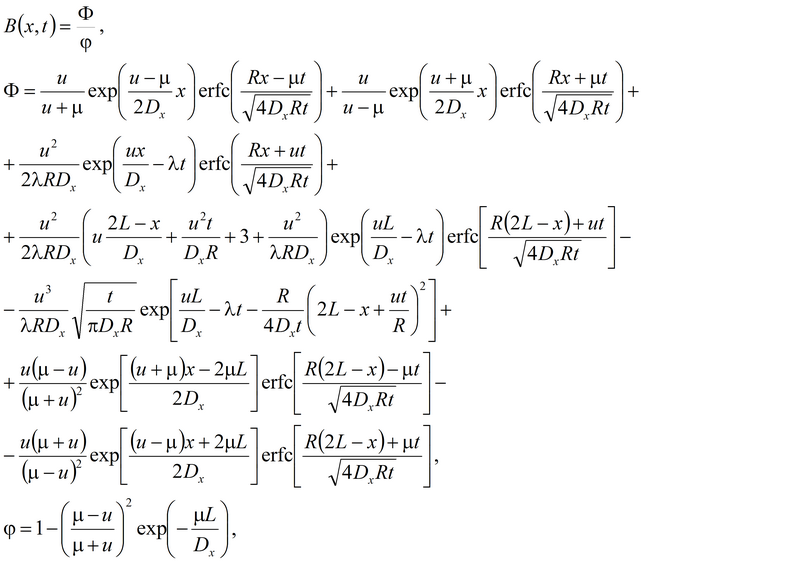
1. Граничное условие I рода: распад, дисперсия, сорбция (Pérez Guerrero et al., 2013):

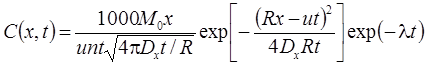
2. Граничное условие III рода: распад, дисперсия, сорбция (Pérez Guerrero et al., 2013):

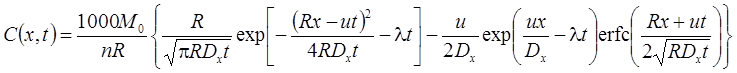
3. Однородный пласт. Линейная неравновесная сорбция: распад, дисперсия, сорбция (Toride et al., 1993):

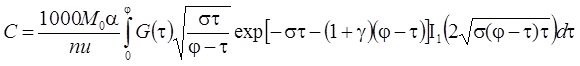
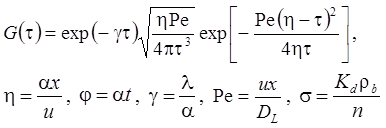
4. Однородный пласт. Линейная неравновесная сорбция: распад, без дисперсии, сорбция (функция Гольдштейна):

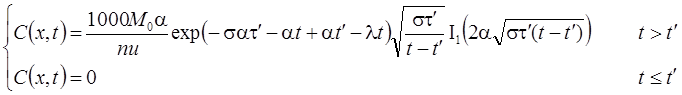
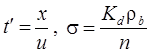
1. Неограниченная емкость блоков (Rumynin, 2011): распад, дисперсия, сорбция (интеграл свертки):

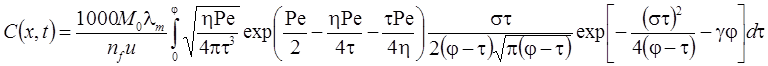
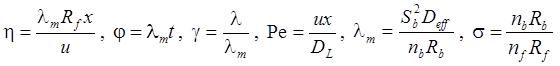
2. Сосредоточенная емкость блоков: распад, дисперсия, сорбция (Toride et al., 1993):

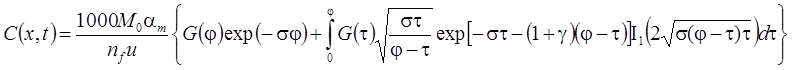
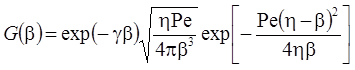
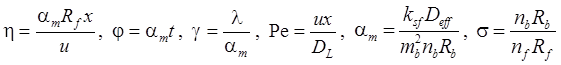
3. Сосредоточенная емкость блоков (Rumynin, 2011): распад, дисперсия, сорбция (интеграл свертки):

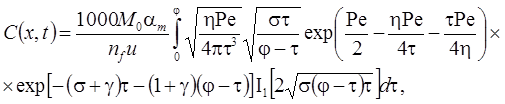
4. Решение задачи в изображениях: распад, дисперсия, сорбция (Rumynin, 2011):

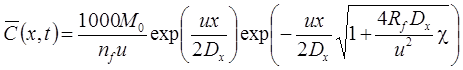
– неограниченная емкость блоков

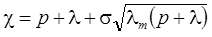
– сосредоточенная емкость блоков

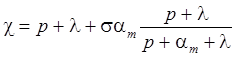
5а. Неограниченная емкость: распад, без дисперсия, сорбция (решение Ловерье):

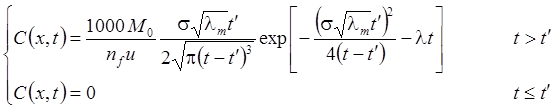
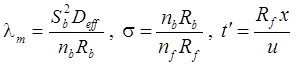
5б. Неограниченная емкость, решение задачи в изображениях: распад, без дисперсия, сорбция:

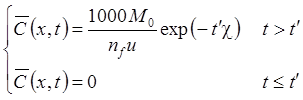
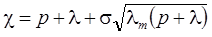
6а. Сосредоточенная емкость: распад, без дисперсия, сорбция (функция Гольдштейна):

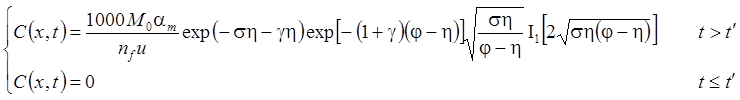
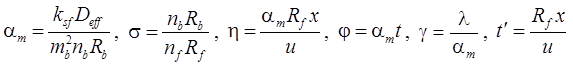
6б. Сосредоточенная емкость, решение задачи в изображениях: распад, без дисперсия, сорбция:

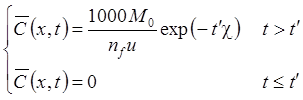
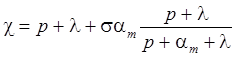
1. Решение для постоянной концетрации на границе, с учетом распада на границе:

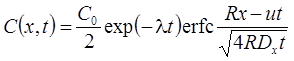
2. Решение для импульса:
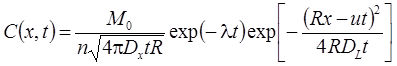