Уравнения нестационарной фильтрации
1) решение Ньюмана для среднего понижения и понижения в пьезометре для совершенной и несовершенной скважины в анизотропном пласте
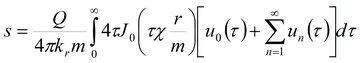
Для решения используется алгоритм программы DELAY2 (автор Neuman, 1986). Условные обозначения смотри:
Neuman S.P. Theory of flow in unconfined aquifers considering delayed gravity response // Water Resources Research. 1972. Vol. 8, N 4. P. 1031–1045.
Neuman S.P. Supplementary comments on "Theory of flow in unconfined aquifers considering delayed gravity response" // Water Resources Research. 1973. Vol. 9, N 4. P. 1102–1103.
Neuman S.P. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response // Water Resources Research. 1974. Vol. 10, N 2. P. 303–312.
Neuman S.P. Analysis of pumping test data from anisotropic unconfined aquifers // Water Resources Research. 1975. Vol. 11, N 2. P. 329–345.
Neuman S.P. Perspective on "Delayed yield" // Water Resources Research. 1979. Vol. 15, N 4. P. 899–908.
2) решения Болтона для среднего понижения и понижения уровня грунтовых вод для совершенной скважины в изотропном пласте
Для среднего понижения (используется два подобных решения Болтона)
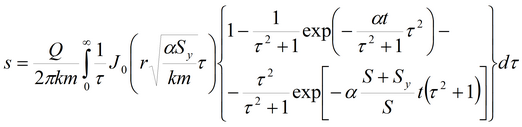
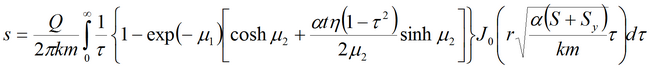
где
эмпирический параметр (1/сут), можно определить как
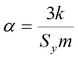
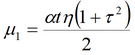
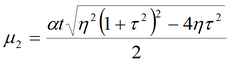
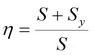
Деривативный анализ:
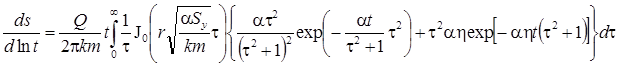
Для понижения уровня грунтовых вод (гравитационный режим)
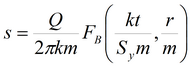
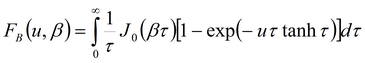
3) решение Менча для среднего понижения и понижения в пьезометре для совершенной и несовершенной скважины в анизотропном пласте
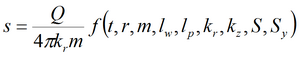
Для решения используется алгоритм программы WTAQ2 (автор Moench, 1997). Смотри:
Moench A.F. Computation of type curves for flow to partially penetrating wells in water-table aquifers // Ground Water. 1993. Vol. 31, N 6. P. 966–971.
Moench A.F. Flow to a well in a water-table aquifer: an improved Laplace transform solution // Ground Water. 1996. Vol. 34, N 4. P. 593–596.
Решение задачи в изображениях
для среднего понижения в наблюдательной скважине
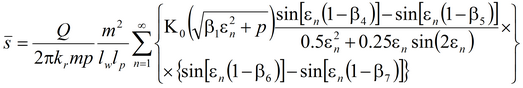
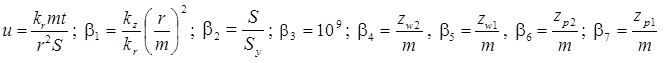
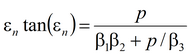
и понижения в пьезометре
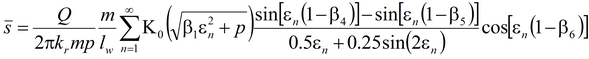
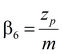
Деривативный анализ (используется преобразование Лапласа функций понижения в наблюдательной скважине или пьезометре):
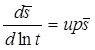
4) решение Менча для среднего понижения и понижения в пьезометре для совершенной и несовершенной скважины в анизотропном пласте с учетом емкости опытной скважины, емкости пьезометра, скин-эффекта опытной скважины и конфигурации пьезометра
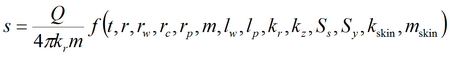
Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Решение задачи в изображениях
для среднего понижения в наблюдательной скважине
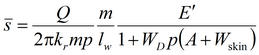
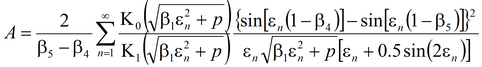
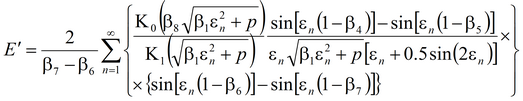
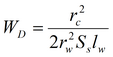
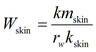
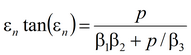
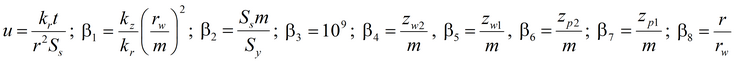
и понижения в пьезометре
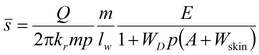
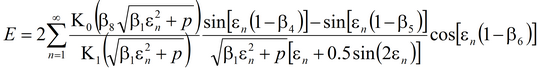
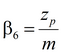
Деривативный анализ (используется преобразование Лапласа функций понижения в наблюдательной скважине или пьезометре):
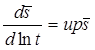
5) решение Менча для понижения в опытной скважине в анизотропном пласте с учетом емкости опытной скважины и скин-эффекта опытной скважины
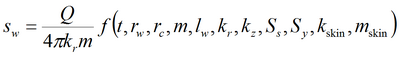
Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Решение задачи в изображениях
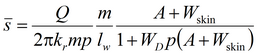
Деривативный анализ (используется преобразование Лапласа функции понижения в опытной скважине):
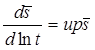
Обозначения см. выше (пункт 4)
Для решений 4 и 5 возможен учет влияния ненасыщенной зоны на понижение в наблюдательной скважине, пьезометре или опытной скважине.
Для решения используется программа WTAQ v.2 (авторы Barlow и Moench, 2011). Смотри:
Barlow P.M., Moench A.F. WTAQ version 2 - a computer program for analysis of aquifer tests in confined and water-table aquifers with alternative representations of drainage from the unsaturated zone. 2011. U.S. Geological Survey. Technique and Methods 3-B9.
Для верхних решений при обработке возможен учет коррекции понижения Джейкоба:
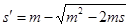
6) упрощенное решение для гравитационного режима для совершенной скважины в изотропном пласте
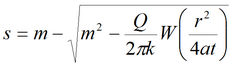
Уравнение для квазистационарного периода:
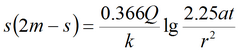
7) упрощенное решение для гравитационного режима для совершенной скважины в изотропном пласте с учетом перетекания через подошву пласта
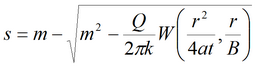
8) решение Менча-Прикета для напорно-безнапорного пласта
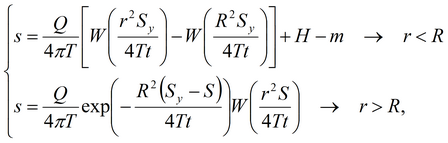
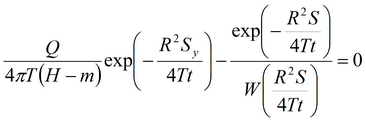
9) решение Боултона-Стрельцовой для безнапорного пласта с двойной емкостью
Решение задачи в изображениях
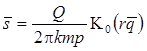
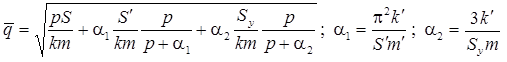
Параметры со штрихом относятся к блоку (m' - размер блока).
Деривативный анализ (используется преобразование Лапласа функции понижения):
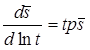
Доступные способы обработки и определяемые параметры
График
|
Способ
|
Параметры
|
Примечание
|
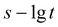
|
подбор
|
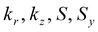
|
|
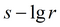
|
подбор
|
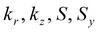
|
подбор по отдельным точкам 1)
|
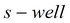
|
подбор
|
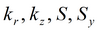
|
подбор по отдельным точкам
|
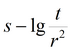
|
подбор
|
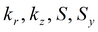
|
|
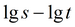
|
подбор
|
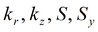
|
|
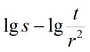
|
подбор
|
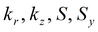
|
|
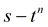
|
подбор
|
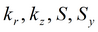
|
|
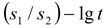
|
подбор
|
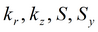
|
|
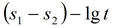
|
подбор
|
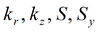
|
|
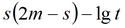
|
прямая
|
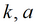
|
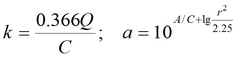
|
подбор
|
|
|
|
прямая
|
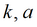
|
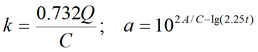
|
подбор
|
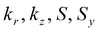
|
|
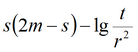
|
прямая
|
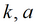
|
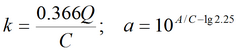
|
подбор
|
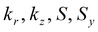
|
|
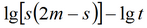
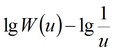
|
эталонная
|
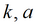
|
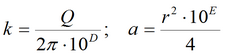
|
подбор
|
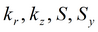
|
|
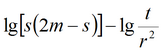
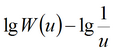
|
эталонная
|
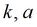
|
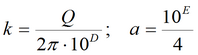
|
подбор
|
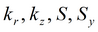
|
|
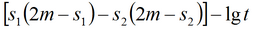
|
прямая
|
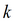
|
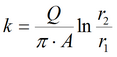
|
подбор
|
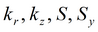
|
|
1) для несовершенных скважин, находящихся на разных отметках.
Для изотропного пласта подбираемые параметры: k, S, Sy.
Для упрощенного решения для гравитационного режима подбираемые параметры: k, a (для пластов без перетекания) или k, a, B (для пластов с учетом перетекания).
Для напорно-безнапорного пласта подбираемые параметры: T, S, Sy.
Для безнапорного пласта с двойной емкостью подбираемые параметры: коэффициент фильтрации и водоотдача трещин и блоков k, S, k', S'.
|