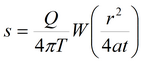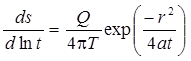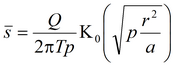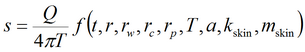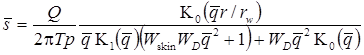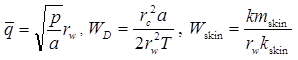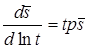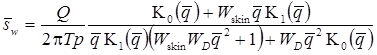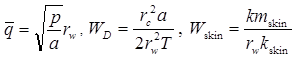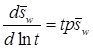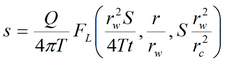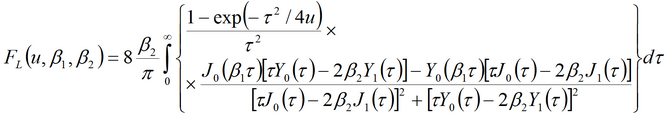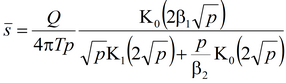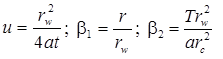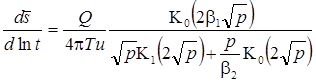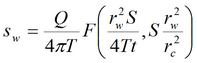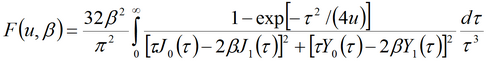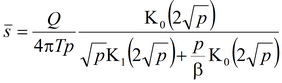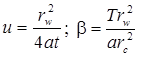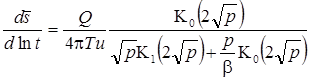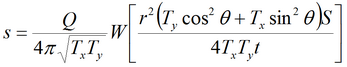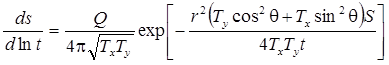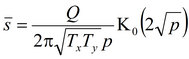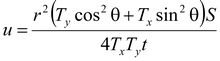Расчетные схемы > Изолированный напорный пласт >Неограниченный в плане пласт |
|
Неограниченный в плане водоносный пласт (схема Тейса)
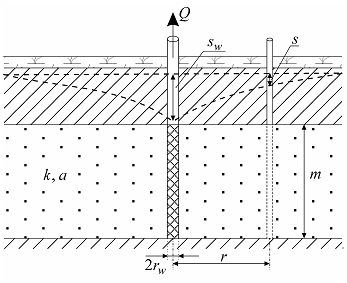
Схема проведения опыта: üводоносный пласт: напорный, изотропный, неограниченный в плане; üпонижение определяется в водоносном пласте на любом расстоянии от опытной скважины; üрежим снижения уровней: два периода – нестационарный и квазистационарный; üможет учитываться емкость опытной скважины, скин-эффект и емкость наблюдательной скважины (см. ниже дополнительные решения).
Типовая схема неограниченного напорного пласта (разрез).
Базовое уравнение:
Деривативный анализ:
Решение задачи в изображениях:
Кроме базового уравнения используются следующие дополнительные решения: 1) решение Менча для понижения в напорном пласте в совершенной наблюдательной скважине; решение учитывает емкость опытной скважины, емкость наблюдательной скважины и скин-эффект опытной скважины
Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри: Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Запись аналогичной задачи в изображениях:
Деривативный анализ:
2) решение Менча для понижения в опытной скважине в напорном пласте; решение учитывает емкость опытной скважины и скин-эффект опытной скважины
Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри: Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Запись аналогичной задачи в изображениях:
Деривативный анализ:
3) решение Пападопулоса для понижения в напорном пласте в совершенной наблюдательной скважине; решение учитывает емкость опытной скважины
Решение задачи в изображениях:
Деривативный анализ:
4) решение Пападопулоса для понижения в опытной скважине в напорном пласте; решение учитывает емкость опытной скважины
Решение задачи в изображениях:
Деривативный анализ:
5) решение Хантуша для планово-анизотропного пласта
Деривативный анализ:
Решение задачи в изображениях:
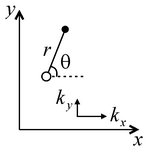
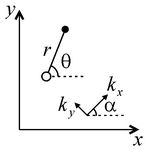
В решении предполагается, что ось абсцисс может не совпадать с направлением анизотропии. Θ – угол между осью x и лучом, направленным от опытной до наблюдательной скважины, градус (задается в таблице "Смещение"). α – угол между направлением анизотропии и координатной осью, градус.
Предусмотрена обработка следующих ОФО: Одна опытная скважина с постоянным расходом Откачка Восстановление уровня изменение уровня отсчитывается от начала откачки изменение уровня отсчитывается от начала восстановления Совместная обработка периода откачки и восстановления Несколько опытных скважин с постоянным расходом Откачка (одновременное начало работы скважин) Восстановление уровня после одновременного начала работы скважин и их одновременной остановки изменение уровня отсчитывается от начала откачки изменение уровня отсчитывается от начала восстановления Совместная обработка периода откачки и восстановления (одновременное начало и окончание работы скважин) Откачка (асинхронное начало работы скважин) Одна опытная скважина с переменным расходом Откачка Несколько опытных скважин с переменным расходом Откачка
Способы обработки приведены только для базового решения. Кроме этого, подбор параметров может осуществляться и по дополнительным решениям. При этом может потребоваться задать такие параметры как радиус обсадной трубы опытной скважины, коэффициент фильтрации скина, толщину скина или конфигурацию наблюдательной скважины.
Литература Cooper H.H., Jacob C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history // Transactions, American Geophysical Union. 1946. Vol. 27, N 4. P. 526–534. Hantush M.S. Analysis of data from pumping tests in anisotropic aquifers // Journal of Geophysical Research. 1966a. Vol. 71, N 2. P. 421–426. Hantush M.S., Thomas R.G. A method for analyzing a drawdown test in anisotropic aquifers // Water Resources Research. 1966. Vol. 2, N 2. P. 281–285. Jacob C.E. Effective radius of drawdown test to determine artesian well // Proceedings of the American Society of Civil Engineers. 1946. Vol. 72, N 5. P. 629–646. Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407. Papadopulos I.S., Cooper H.H. Drawdown in a well of large diameter // Water Resources Research. 1967. Vol. 3, N 1. P. 241–244. Theis C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage // Transactions, American Geophysical Union. 1935. Vol. 35, pt. 2. P. 519–524.
|