Уравнения нестационарной фильтрации
1. Решение, полученное на основе суперпозиции:
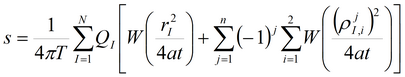
2. Решение на основе функции Грина:
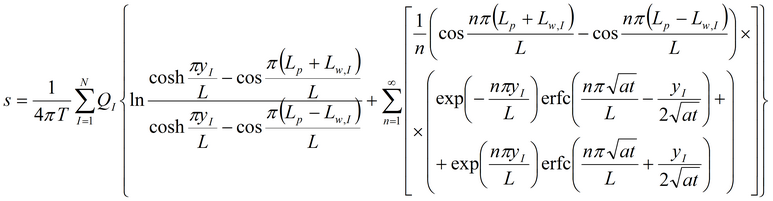
где
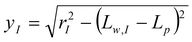
3. Второе решение на основе функции Грина (из функции Грина для пласта с перетеканием): решение строится аналогично первому уравнению для функции Грина.
Уравнения для стационарного периода
1. Решение, полученное на основе суперпозиции:
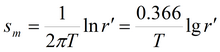
где
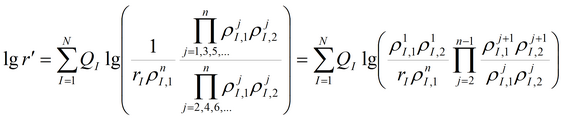
2. Решение на основе функции Грина:
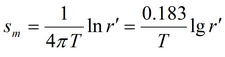
где
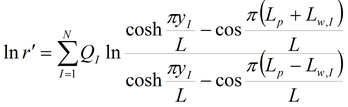
Доступные способы обработки и определяемые параметры
График
|
Способ
|
Параметры
|
Примечание
|
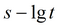
|
прямая 1)
|
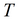
|
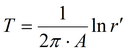
|
подбор
|
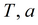
|
|
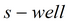
|
подбор
|
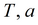
|
подбор по отдельным точкам
|
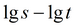
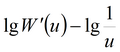
|
эталонная
|
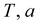
|
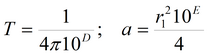
|
подбор
|
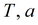
|
|
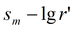
|
прямая 2)
|
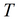
|
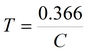
|

|
подбор
|
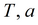
|
|
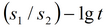
|
подбор
|
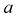
|
|

|
прямая 1)
|
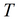
|
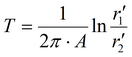
|
подбор
|
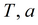
|
|
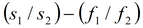
|
биссектриса
|
|
|
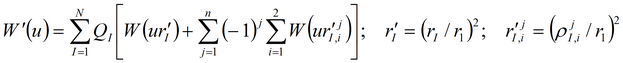
Можно приводить к расстоянию до любой опытной скважины (расстояние до этой опытной скважины используется при определении пьезопроводности по способу эталонной кривой).
При обработке используется принцип суперпозиции или функция Грина.
1) по понижениям на период стационара (при использовании функции Грина значение проводимости в два раза меньше);
2) строится график только по формуле, основанной на принципе суперпозиции.
|