Уравнения нестационарной фильтрации
1. Решение, полученное на основе суперпозиции:
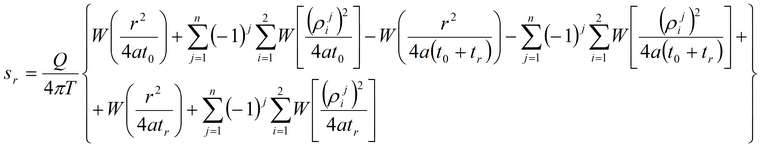
2. Решение на основе функции Грина:
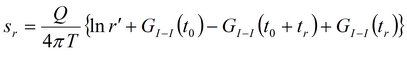
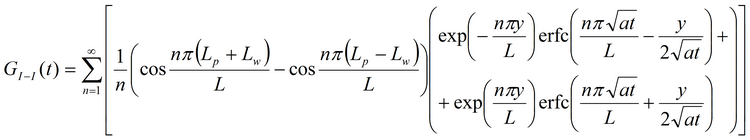
3. Второе решение на основе функции Грина:
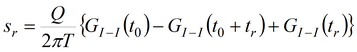
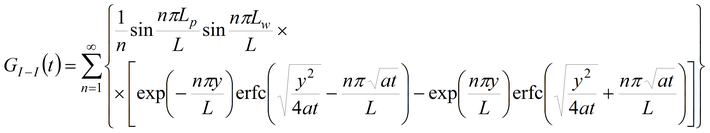
где

Уравнения для стационарного периода
1. Решение, полученное на основе суперпозиции:
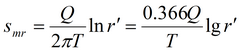
где
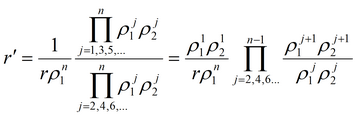
2. Решение на основе функции Грина:
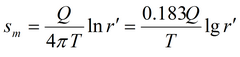
где
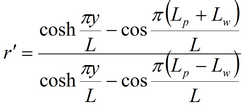
Доступные способы обработки и определяемые параметры
График
|
Способ
|
Параметры
|
Примечание
|
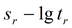
|
прямая 1)
|

|
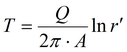
|
подбор
|
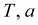
|
|
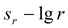
|
подбор
|
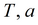
|
подбор по отдельным точкам
|
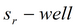
|
подбор
|
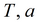
|
подбор по отдельным точкам
|
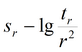
|
подбор
|
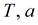
|
|
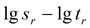
|
подбор
|
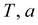
|
|
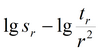
|
подбор
|
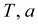
|
|
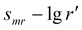
|
прямая 2)
|
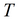
|
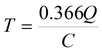
|
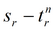
|
подбор
|
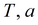
|
|
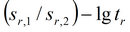
|
подбор
|
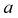
|
|
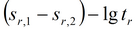
|
прямая 1)
|
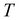
|
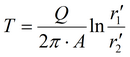
|
подбор
|
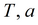
|
|
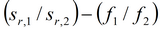
|
биссектриса
|
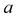
|
|
При обработке используется принцип суперпозиции или функция Грина. Для функции Грина необходимо увеличить количество слагаемых в ряду.
1) по прямолинейному участку, отвечающему конечным значениям восстановления (при использовании функции Грина значение проводимости в два раза меньше);
2) строится график только по формуле, основанной на принципе суперпозиции.
|