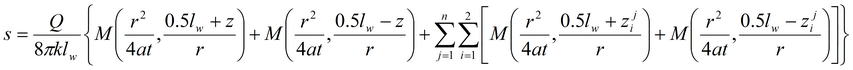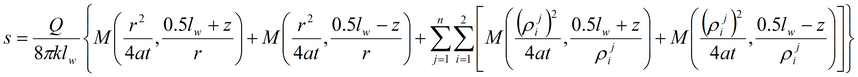Расчетные схемы > Линейный источник > Ограниченный пласт >

Границы II рода

Линейный источник в ограниченном в разрезе или плане водоносном пласте: границы II рода

Схема проведения опыта:

üобщие условия для линейного источника в ограниченном водоносном пласте;

üграницы: две профильные или плановые непроницаемые (условия II рода);

üесли границы располагаются в разрезе, то принимается неограниченность пласта в плане и, наоборот, если имеются плановые границы, то пласт неограничен в разрезе;

üфиктивные скважины: ряд бесконечных скважин, знаки расходов см. на рисунке;

üможет учитываться емкость опытной скважины, скин-эффект и емкость наблюдательной скважины (см. решения Менча с учетом емкости опытной скважины).

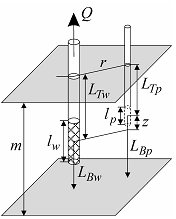
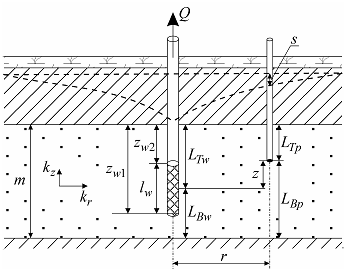
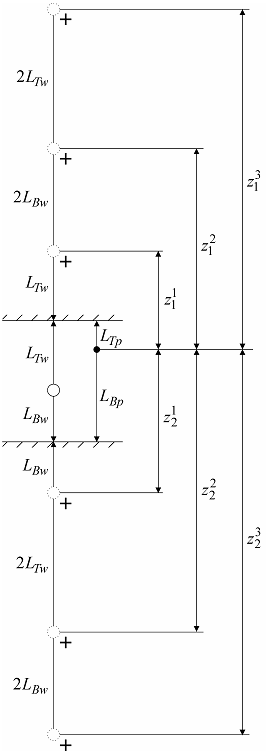
Типовая схема линейного источника в напорном ограниченном в разрезе пласте.

а – трехмерное представление; б – схематичный разрез с пьезометром; в – схематичный разрез с наблюдательной скважиной; г – схематичный разрез с фиктивными скважинами и вертикальными расстояниями до них.

Откачка из опытной скважины, вскрывающей водоносный пласт своим дном (опытная скважина примыкает к кровле пласта).

Типовая схема линейного источника в пласте-полосе с параллельными непроницаемыми границами: трехмерное представление и план.

Базовые уравнения:

Граница в разрезе, пласт неограничен в плане:

Граница в плане, пласт неограничен в разрезе:

Кроме базового уравнения для границы в разрезе используются следующие дополнительные решения:

1) решения Хантуша для понижения в напорном анизотропном пласте в несовершенной скважине или пьезометре

2) решение Менча для понижения в напорном анизотропном пласте в несовершенной скважине или пьезометре; решение учитывает емкость опытной скважины, емкость наблюдательной  скважины или пьезометра и скин-эффект опытной скважины.

Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри:

Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.

3) решение Менча для понижения в опытной несовершенной скважине в напорном анизотропном пласте; решение учитывает емкость опытной скважины и скин-эффект опытной скважины.

Для решения используется алгоритм программы WTAQ3 (автор Moench, 1997). Смотри:

Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.

Предусмотрена обработка следующих ОФО:

Одна опытная скважина с постоянным расходом

Откачка

Восстановление уровня

Одна или несколько опытных скважин с переменным расходом

Откачка

Литература

Hantush M.S. Drawdown around a partially penetrating well // Journal of the Hydraulics Division. Proceedings of the American Society of Civil Engineers. 1961b. Vol. 87, N HY4. P. 83–98.

Moench A.F. Computation of type curves for flow to partially penetrating wells in water-table aquifers // Ground Water. 1993. Vol. 31, N 6. P. 966–971.

Moench A.F. Flow to a well in a water-table aquifer: an improved Laplace transform solution // Ground Water. 1996. Vol. 34, N 4. P. 593–596.

Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.

Hantush M.S. Non-steady flow to a well partially penetrating an infinite leaky aquifer // Proceedings of the Iraqi scientific societies. 1957. Vol. 1. P. 10–19.

Mishra P.K., Vesselinov V.V., Neuman S.P. Radial flow to a partially penetrating well with storage in an anisotropic confined aquifer // Journal of hydrology. 2012. Vol. 448–449. P. 255–259.