Уравнения нестационарной фильтрации
В смежном пласте уровень постоянный
Понижение в основном пласте
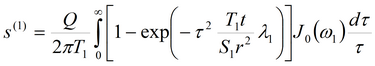
где
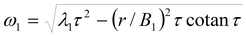
Понижение в разделяющем слое
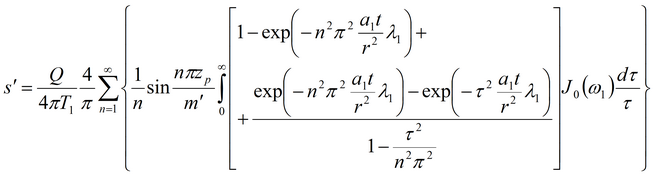
Решение задачи в изображениях для понижения в основном пласте и разделяющем слое:
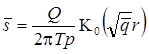

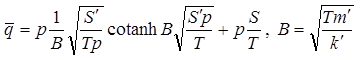
Деривативный анализ (используется преобразование Лапласа функции понижения в основном пласте):
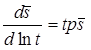
Понижение в разделяющем слое при незначительном перетекании (понижение в основном пласте описывается решением Тейса, несмотря на незначительное движение воды через разделяющий слой)
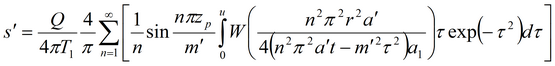
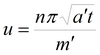
или аппроксимация для больших моментов времени

где zp – расстояние от точки наблюдения в разделяющем слое до кровли (или подошвы) основного пласта, м.
В смежном пласте уровень меняется
Понижение в основном пласте (с опытной скважиной)

Понижение в смежном пласте (без опытной скважины)

Понижение в разделяющем слое
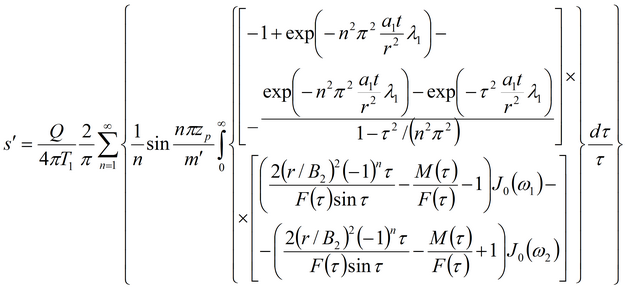
где
Решение задачи в изображениях для понижения в основном пласте, смежном пласте и разделяющем слое:
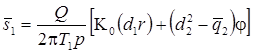
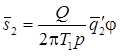
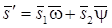

Деривативный анализ (используется преобразование Лапласа функций понижения в основном и смежном пластах):
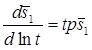

Для понижения в полуограниченном слабопроницаемом слое
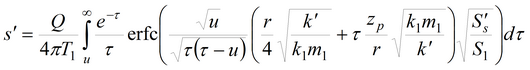
где
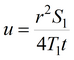
Понижение в полуограниченном слабопроницаемом слое при незначительном перетекании (понижение в основном пласте описывается решением Тейса, несмотря на незначительное движение воды через разделяющий слой)
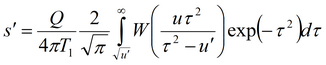
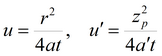
или аппроксимация для больших моментов времени
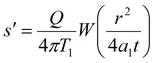
Доступные способы обработки и определяемые параметры
График
|
Способ
|
Параметры
|
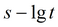
|
подбор
|

|
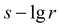
|

|
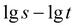
|

|

|
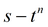
|

|

|
Параметры определяются как по понижению в основном пласте, так и по понижению в смежном пласте.
Для варианта постоянного уровня в смежном пласте определяемые параметры:
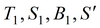
Для схемы полуограниченного в разрезе слабопроницаемого слоя определяемые параметры:

Для понижения в слабопроницаемом слое при незначительном перетекании определяемые параметры:

а для их аппроксимаций на большие моменты времени
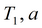
|