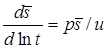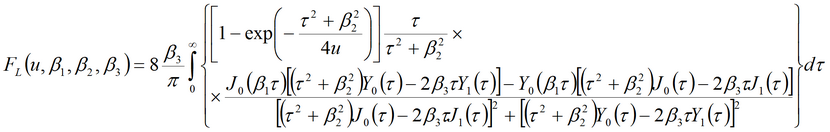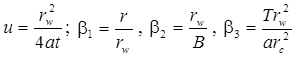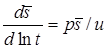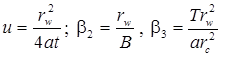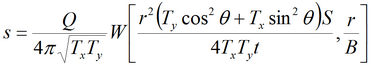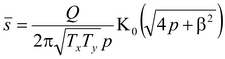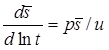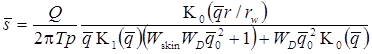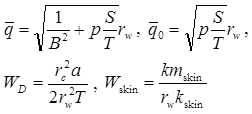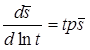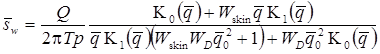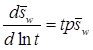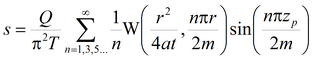Расчетные схемы > Водоносный комплекс с перетеканием > Постоянный уровень в смежном пласте >

Неограниченный в плане пласт

Неограниченный в плане пласт

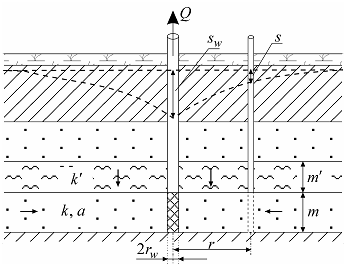
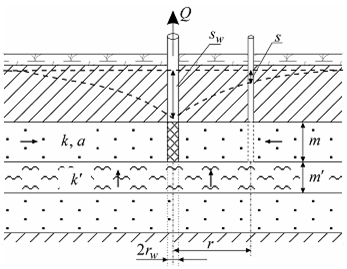
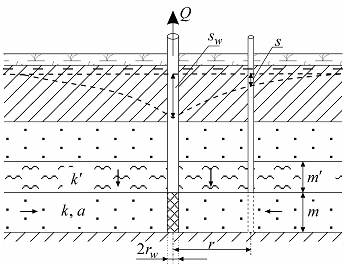
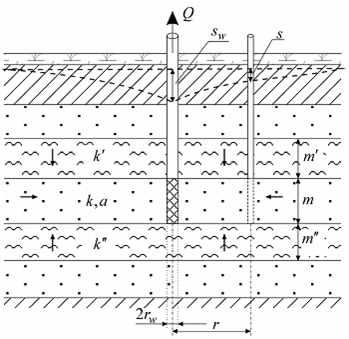
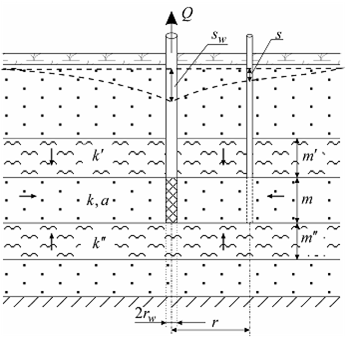
Схема проведения опыта:

üводоносный комплекс: состоит из переслаивающихся хорошо и слабопроницаемых изотропных слоев;

üосновной водоносный пласт: хорошо проницаемый слой, в котором находится опытная скважина и определяется понижение;

üсмежный водоносный пласт: один или два хорошо проницаемых слоя, уровень в котором не меняется в процессе опробования;

üначальные уровни в хорошо проницаемых водоносных пластах могут как совпадать, так и быть различными;

üразделяющий слой: один или два слабопроницаемых слоя, через который происходит перетекание;

üграница: водоносный комплекс неограничен в плане;

üопытная скважина: совершенная по степени вскрытия, находится в основном хорошо проницаемом пласте, емкость скважины может учитываться;

üпонижение определяется на любом расстоянии от опытной скважины в основном хорошо проницаемом пласте;

üпоток в слабопроницаемых слоях вертикальный;

üупругий режим в слабопроницаемых слоях не учитывается;

üможет учитываться емкость опытной скважины и скин-ээффект (см. ниже дополнительные решения).

Отдельно рассмотрена задача откачки из водоносного пласта, расположенного под рекой (см. ниже решение 6).

а        б

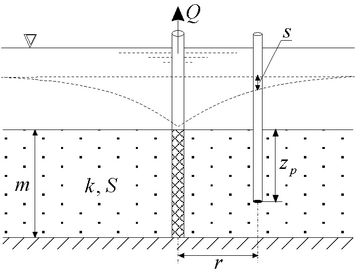
в        г

д        е

Типовые схемы водоносного пласта с перетеканием (разрезы), уровень в смежных пластах не меняется в процессе опробования.

а – трехслойный напорный комплекс с перетеканием через кровлю, б – через подошву пласта;
в – пример трехслойного напорного комплекса с различными начальными уровнями в хорошо проницаемых пластах; г – трехслойный безнапорный комплекс с перетеканием через кровлю пласта; д, е – пятислойные напорный (д) и безнапорный (е) комплексы с перетеканием через кровлю и через подошву пласта.
Стрелками показаны направления потока в слоях.

Базовое уравнение:

Деривативный анализ:

Решение задачи в изображениях:

Деривативный анализ:

или с использованием преобразования Лапласа функции понижения

Кроме базового уравнения используются следующие дополнительные решения:

1) решение для понижения в пласте с перетеканием в совершенной наблюдательной скважине; решение учитывает емкость опытной скважины

Решение задачи в изображениях:

Деривативный анализ (используется преобразование Лапласа функции понижения):

2) решение для понижения в опытной скважине в пласте с перетеканием; решение учитывает емкость опытной скважины

Решение задачи в изображениях:

Деривативный анализ (используется преобразование Лапласа функции понижения):

3) решение Хантуша для планово-анизотропного пласта

Решение задачи в изображениях:

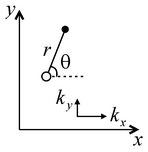
В решении предполагается, что ось абсцисс может не совпадать с направлением анизотропии. Θ – угол между осью x и лучом, направленным от опытной до наблюдательной скважины, градус. α – угол между направлением анизотропии и координатной осью, градус.

Деривативный анализ (используется преобразование Лапласа функции понижения):

4) решение для понижения в наблюдательной скважине с учетом емкости оптытной скважины и скин-эффекта:

Деривативный анализ:

5) решение для понижения в опытной скважине с учетом ее емкости и скин-эффекта:

Деривативный анализ:

6) решение для понижения в пьезометре при откачке из водоносного пласта, расположенного под рекой:

Схема откачки из водоносного пласта, расположенного под рекой.

Предусмотрена обработка следующих ОФО:

Одна опытная скважина с постоянным расходом

Откачка

Восстановление уровня

Несколько опытных скважин с переменным расходом

Откачка

Способы обработки приведены только для базового решения. Кроме этого, подбор параметров может осуществляться  и по дополнительным решениям. При этом может потребоваться задать радиус обсадной трубы опытной скважины.

Литература

Hantush M.S. Analysis of data from pumping tests in anisotropic aquifers // Journal of Geophysical Research. 1966. Vol. 71, N 2. P. 421–426.

Hantush M.S., Jacob C.E. Non-steady radial flow in an infinite leaky aquifer // Transactions, American Geophysical Union. 1955. Vol. 36, N 1. P. 95–100.

Hantush M.S., Thomas R.G. A method for analyzing a drawdown test in anisotropic aquifers // Water Resources Research. 1966. Vol. 2, N 2. P. 281–285.

Jacob C.E. Radial flow in a leaky artesian aquifer // Transactions, American Geophysical Union. 1946. Vol. 27, N 2. P. 198–205.

Lai R.Y.S., Chen-Wu Su. Nonsteady flow to a large well in a leaky aquifer // Journal of Hydrology. 1974. Vol. 22, N 3/4. P. 333–345.

Bruggeman G.A. Analytical solutions of geohydrological problems. Developments in water science 46. Elsevier, The Netherlands, 1999.