Уравнения нестационарной фильтрации
Одна опытная скважина с постоянным расходом. Решения получены на основе базового решения
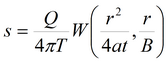
с учетом влияния фиктивных скважин (использовался принцип суперпозиции).
Кроме базового решения для ограниченный пластов используются нестационарные решения, полученные на основе функций Грина:
пласт-полоса (границы I рода)
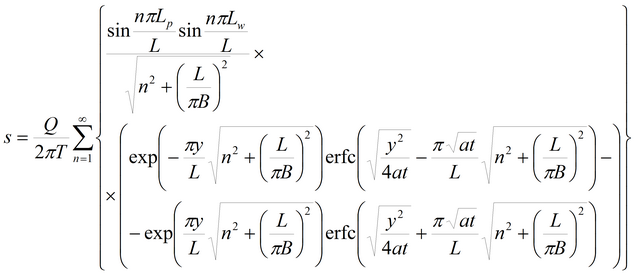
пласт-полоса (границы II рода)
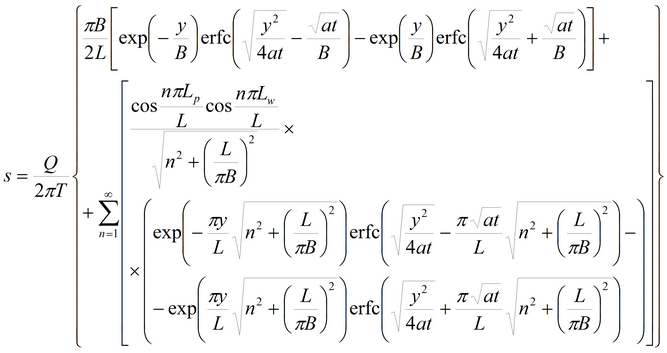
Уравнения для стационарного периода
Полуограниченный пласт (граница I рода)
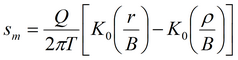
Полуограниченный пласт (граница II рода)
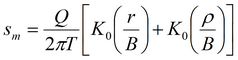
Пласт-полоса (границы I рода): решение на основе суперпозиции и на основе функции Грина
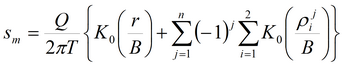
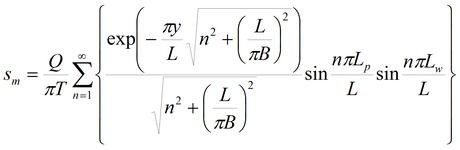
Пласт-полоса (границы II рода): решение на основе суперпозиции и на основе функции Грина
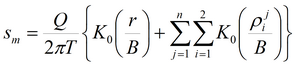
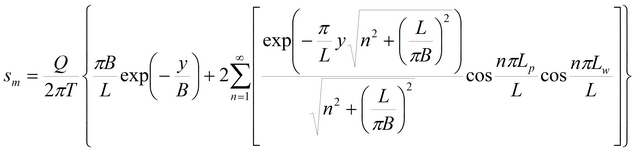
Пласт-полоса (границы I и II рода): решение на основе суперпозиции и на основе функции Грина
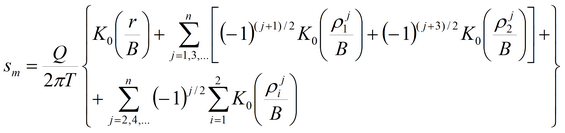
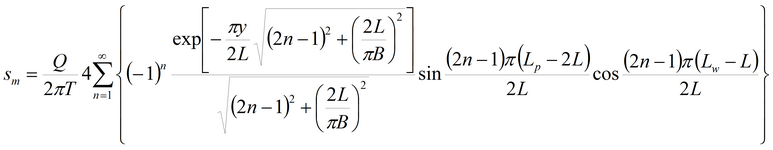
Для нескольких опытных скважин с переменным расходом кроме влияния фиктивных скважин в решении учитывалось влияние произвольного числа опытных скважин и изменение расхода в каждой из них.
Доступные способы обработки и определяемые параметры
График
|
Способ
|
Параметры
|
Примечание
|
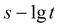
|
прямая 1)
|
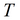
|
|
горизонтальная прямая по данным деривативного анализа 2)
|
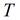
|
Для полуограниченного пласта (граница I рода):
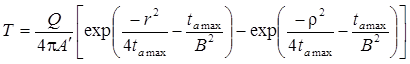
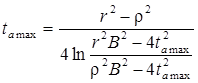
Для полуограниченного пласта (граница II рода):
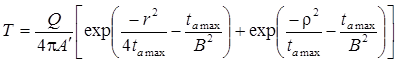
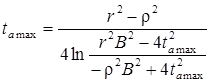
|
подбор
|
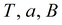
|
|
подбор по данным деривативного анализа
|
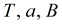
|
|
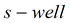
|
подбор
|
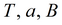
|
подбор по отдельным точкам
|
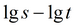
|
подбор
|
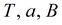
|
|
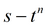
|
подбор
|
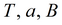
|
|
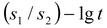
|
подбор
|
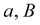
|
|
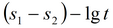
|
подбор
|
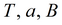
|
|
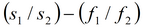
|
биссектриса
|
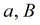
|
|
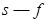
|
прямая
|
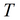
|
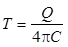
|
построение оси X
|
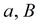
|
Все замеры должны быть на одной прямой, выходящей из начала координат
|
1) на период стационара при заданном параметре перетекания B; определение проводимости зависит от граничных условий (см. уравнения выше для стационарного периода),
2) при заданном параметре перетекания B
|