Linear source in a bounded aquifer: no-flow boundaries
Assumptions:
✓general assumptions for linear source in a bounded (strip) aquifer;
✓two no-flow boundaries either lateral or profile (Neumann);
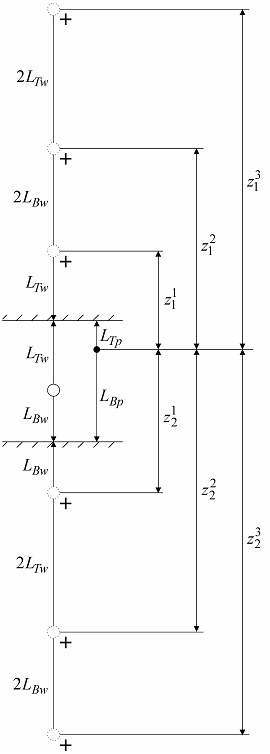
✓image wells form an infinite row, signs of rates shown in figure below;
✓storage capacity both of pumping and observation wells as well as skin factor could be taken into account (see Moench’s solutions accounting for pumping well storage capacity).
a b c |
d
|
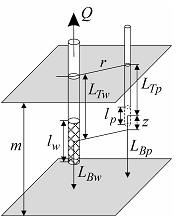
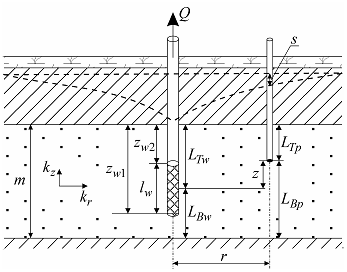
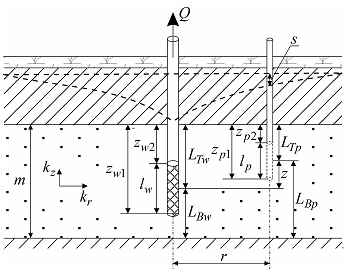
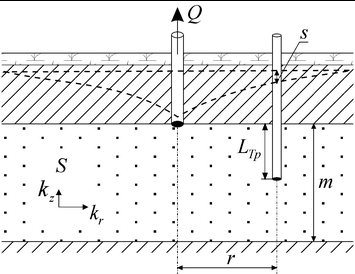
Linear source in the confined aquifer with profile boundaries.
a – 3D view, b – schematic cross-section with a piezometer; c – schematic cross-section with an observation well; d - schematic cross-section showing image wells and their vertical distances.
Pumping well just tapping the aquifer
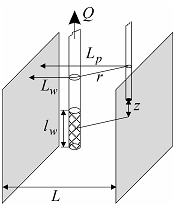

Linear source in the strip-aquifer with parallel no-flow boundaries: 3D and plan views.
Fundamental equations:
Aquifer with a profile boundaries, of infinite lateral extent:
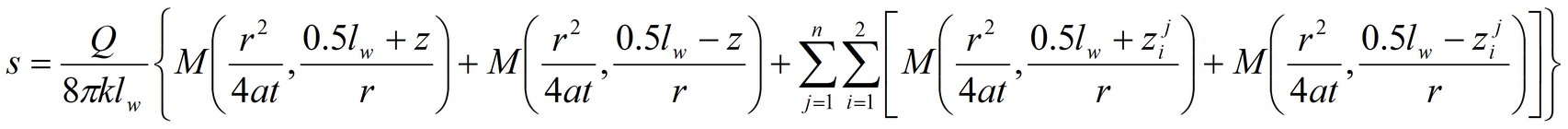
Lateral boundaries:
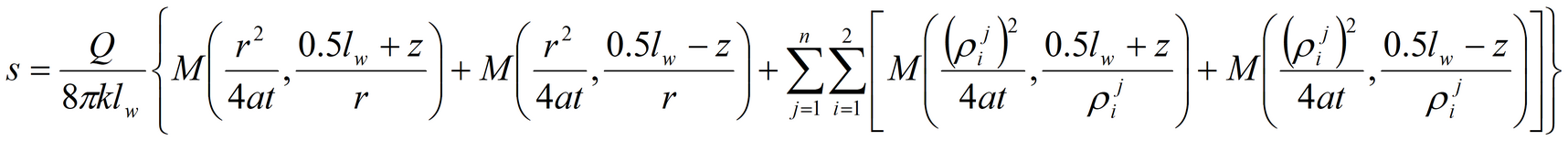
Besides the fundamental equation (for aquifer with a profile boundary) the following complementary solutions are applied:
1) Hantush's solution for drawdown in a partially penetrating observation well or a piezometer in the confined anisotropic aquifer
2) Moench"s solution for drawdown in a partially penetrating observation well or a piezometer in the confined anisotropic aquifer; the solution takes into account the storage capacity of the pumping well, the storage capacity of the observation well or piezometer and the skin-factor of the pumping well
Code of WTAQ3 program is used for calculation (author Moench, 1997). See:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
3) Moench solution for drawdown in the pumping partially penetrating well in the confined anisotropic aquifer; the solution takes into account the storage capacity and the skin-factor of the pumping well.
Code of WTAQ3 program is used for calculation (author Moench, 1997). See:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Pumping regimes:
One well pumped at a constant rate
Pumping
Recovery
One or several wells pumped at a variable rate
Pumping
References
Hantush M.S. Drawdown around a partially penetrating well // Journal of the Hydraulics Division. Proceedings of the American Society of Civil Engineers. 1961b. Vol. 87, N HY4. P. 83–98.
Moench A.F. Computation of type curves for flow to partially penetrating wells in water-table aquifers // Ground Water. 1993. Vol. 31, N 6. P. 966–971.
Moench A.F. Flow to a well in a water-table aquifer: an improved Laplace transform solution // Ground Water. 1996. Vol. 34, N 4. P. 593–596.
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Hantush M.S. Non-steady flow to a well partially penetrating an infinite leaky aquifer // Proceedings of the Iraqi scientific societies. 1957. Vol. 1. P. 10–19.
Mishra P.K., Vesselinov V.V., Neuman S.P. Radial flow to a partially penetrating well with storage in an anisotropic confined aquifer // Journal of hydrology. 2012. Vol. 448–449. P. 255–259.