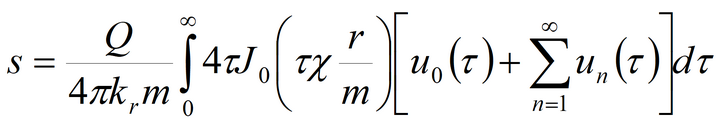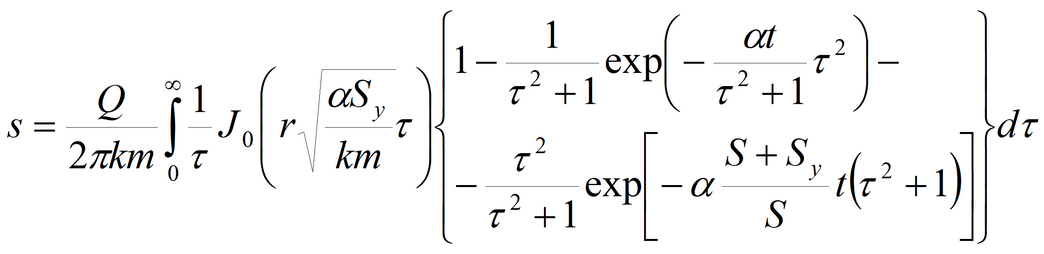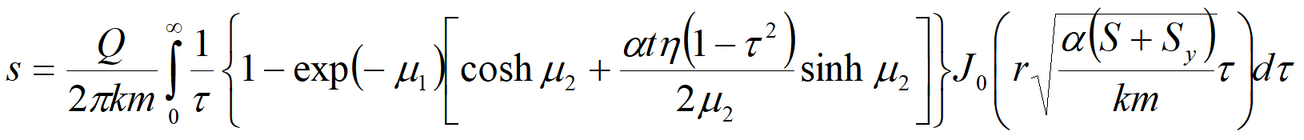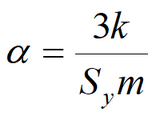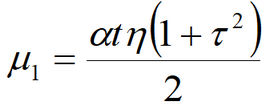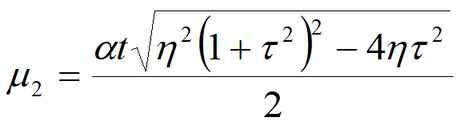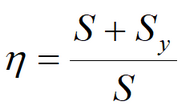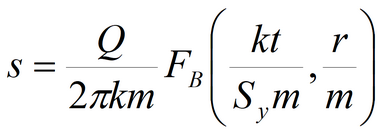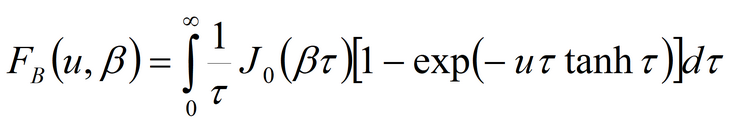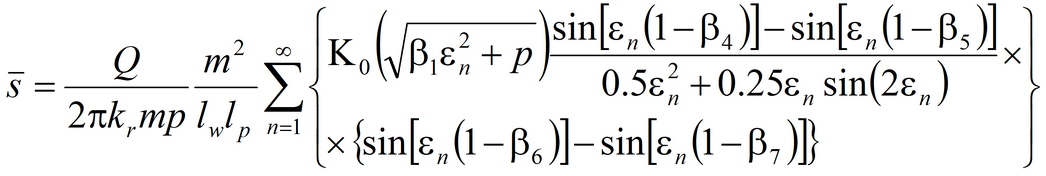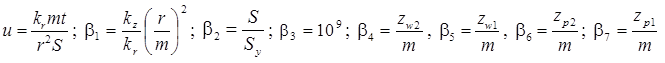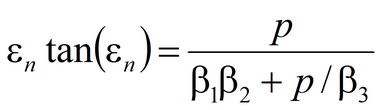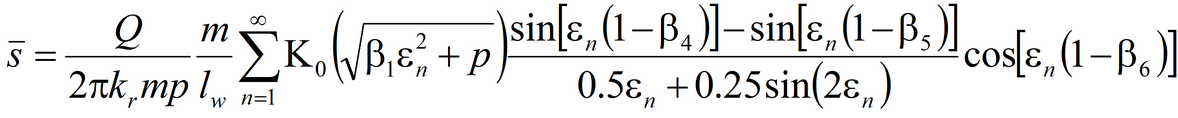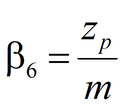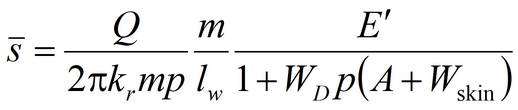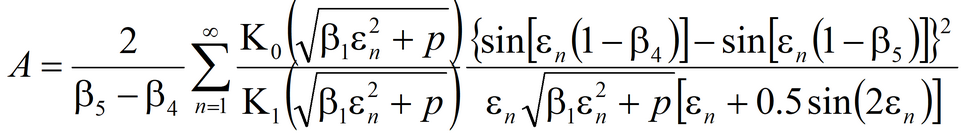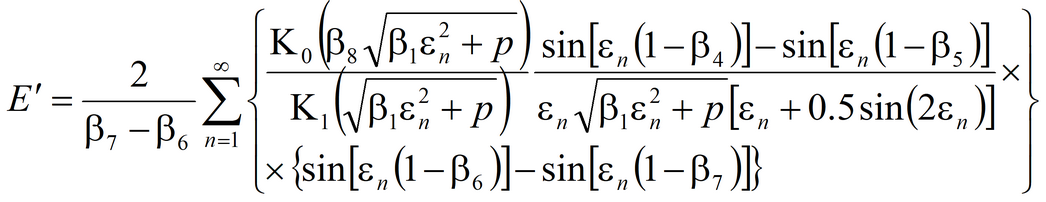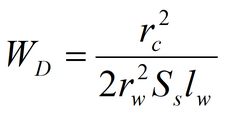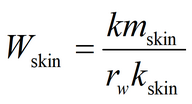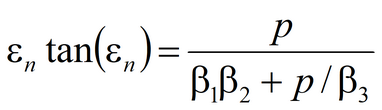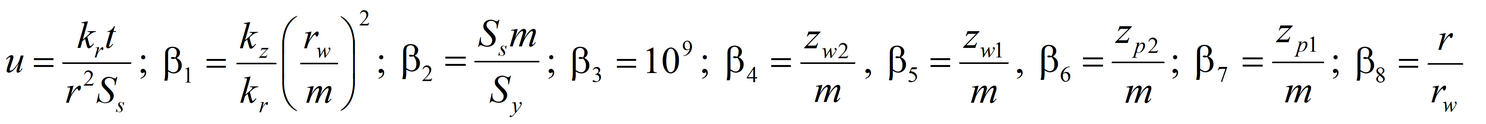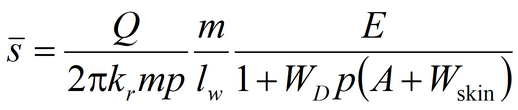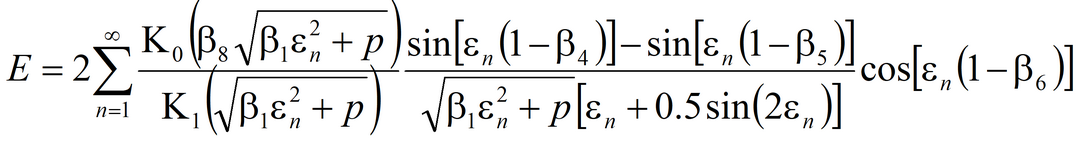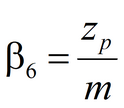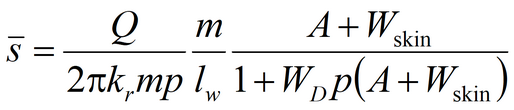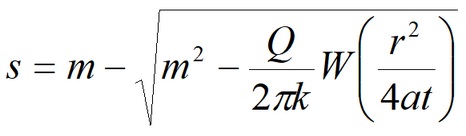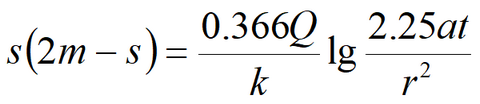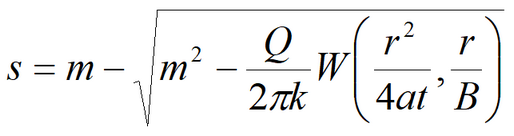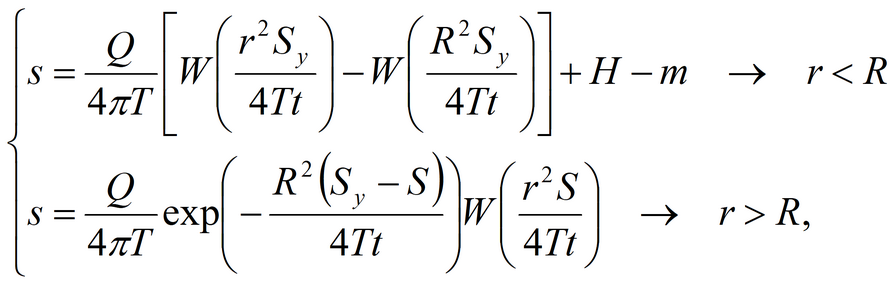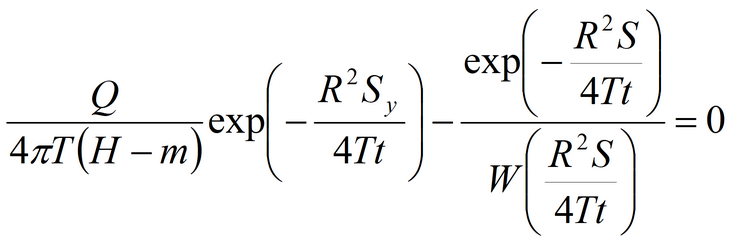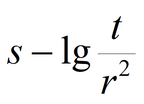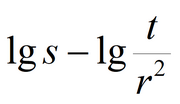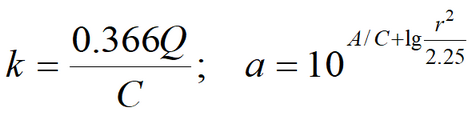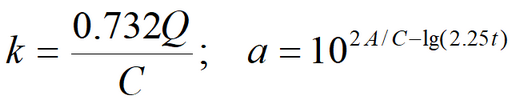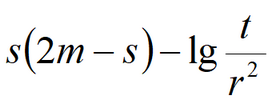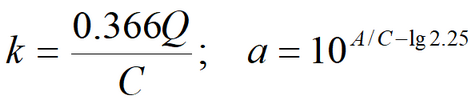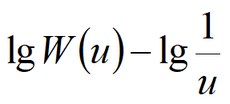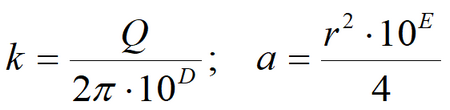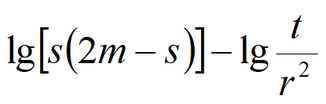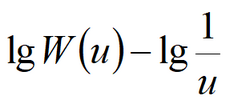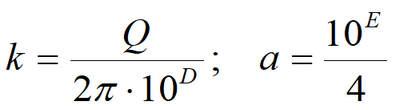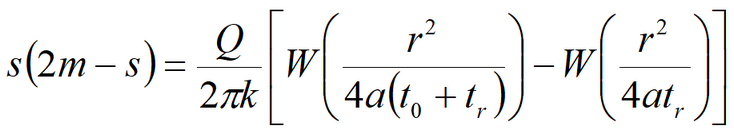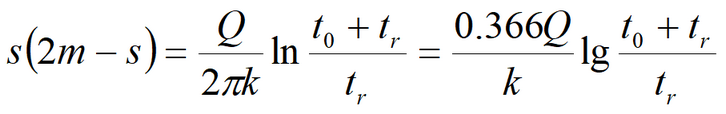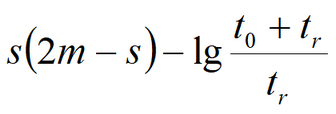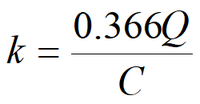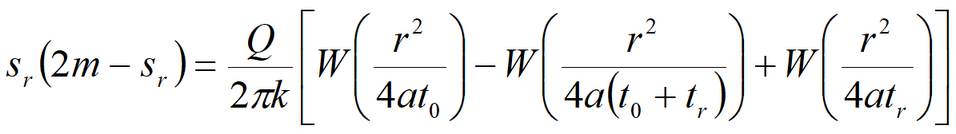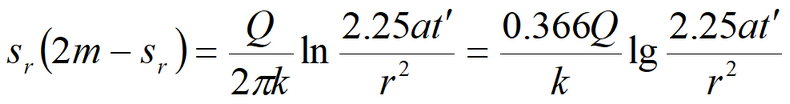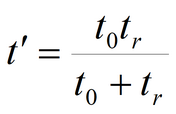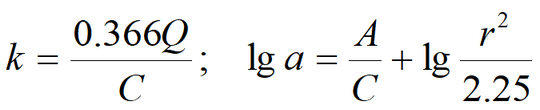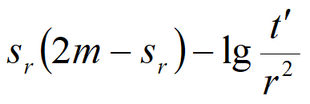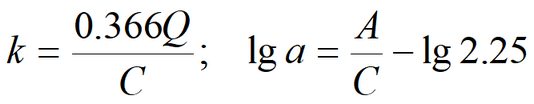Analytical equations and methods for aquifer test analysis
Unsteady-state flow equations 1) Neuman’s solution for average drawdown in observation well and drawdown in piezometer in anisotropic aquifer; pumping well and observation well being fully penetrating or partially penetrating
The code of DELAY2 program is used (Neuman, 1986). For explanations see: Neuman S.P. Theory of flow in unconfined aquifers considering delayed gravity response // Water Resources Research. 1972. Vol. 8, N 4. P. 1031–1045. Neuman S.P. Supplementary comments on «Theory of flow in unconfined aquifers considering delayed gravity response» // Water Resources Research. 1973. Vol. 9, N 4. P. 1102–1103. Neuman S.P. Effect of partial penetration on flow in unconfined aquifers considering delayed gravity response // Water Resources Research. 1974. Vol. 10, N 2. P. 303–312. Neuman S.P. Analysis of pumping test data from anisotropic unconfined aquifers // Water Resources Research. 1975. Vol. 11, N 2. P. 329–345. Neuman S.P. Perspective on «Delayed yield» // Water Resources Research. 1979. Vol. 15, N 4. P. 899–908. 2) Boulton’s solutions for average drawdown and water table drawdown in fully penetrating well in isotropic aquifer Two related Boulton’s solutions being used, average drawdown is written as
where Empirical constant (1/d) is
Water table drawdown equation reads
3) Moench’s solution for average drawdown in observation well and drawdown in piezometer in anisotropic aquifer; pumping well and observation well being fully penetrating or partially penetrating The code of WTAQ2 program is used (Moench, 1995).See: Moench A.F. Computation of type curves for flow to partially penetrating wells in water-table aquifers // Ground Water. 1993. Vol. 31, N 6. P. 966–971. Moench A.F. Flow to a well in a water-table aquifer: an improved Laplace transform solution // Ground Water. 1996. Vol. 34, N 4. P. 593–596.
Laplace transform solution: for observation well
for piezometer
4) Moench’s solution for average drawdown in observation well and drawdown in piezometer in anisotropic aquifer with account for pumping well storage capacity, piezometer storage capacity, skin effect in the pumping well and shape factor of the piezometer The code of WTAQ3 program is used (Moench, 1997).See: Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Laplace transform solution: for observation well
for piezometer
5) Moench’s solution for drawdown in pumping well in anisotropic aquifer with account for pumping well storage capacity and skin effect The code of WTAQ3 program is used (Moench, 1997).See: Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Laplace transform solution:
6) Simplified solution for water table drawdown in fully penetrating well in isotropic aquifer
Equation for quasi-steady-state flow period:
7) Simplified solution for water table drawdown in fully penetrating well in isotropic leaky aquifer
8) Moench-Prickett solution for confined-unconfined aquifer
Methods of analysis and parameters being estimated
1) when screens of partially penetrating wells have different elevations. Parameters matched for the case of isotropic aquifer are: k, S, Sy. Parameters matched in simplified solution for water table drawdown are: k, a (nonleaky aquifer) or k, a, B (leaky aquifer). Parameters matched for confined-unconfined aquifer: T, S, Sy. |
|
|