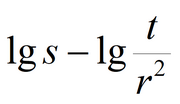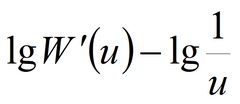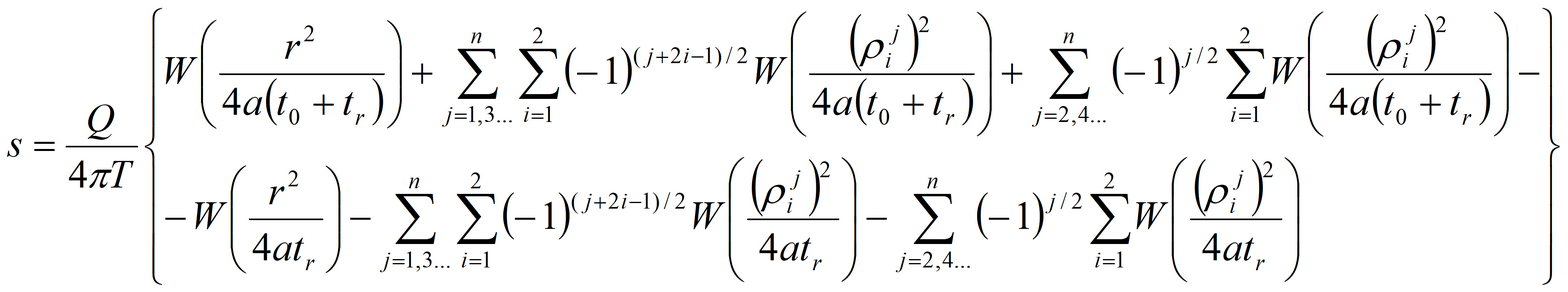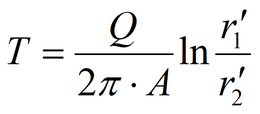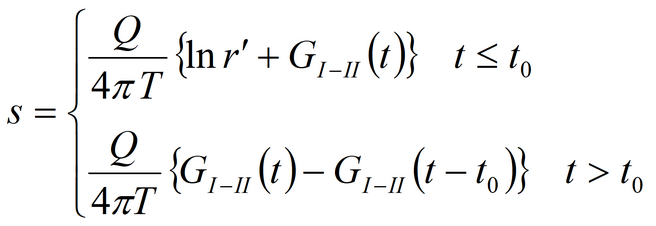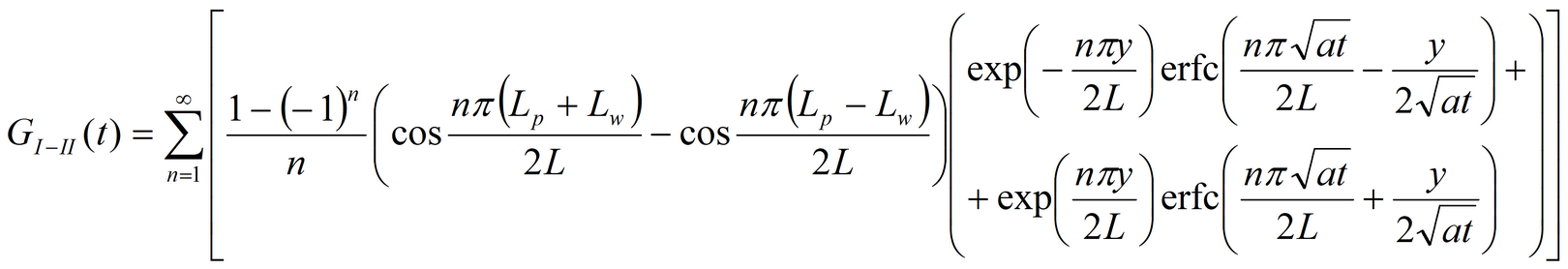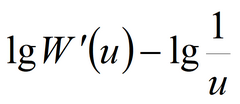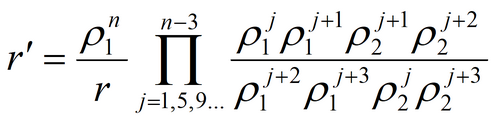Unsteady-state flow equations

1. Superposition principle:

2. Green’s function:

where

Steady-state flow equations

1. Superposition principle:

where

2. Green’s function:

where

Methods of analysis and parameters being estimated

Analysis is based either on the superposition principle or on Green’s function.

1) use steady-state (the transmissivity value calculated using Green’s function would be twice lower);

2) the graph is plotted only for the equation based on superposition principle.

Unsteady-state flow equations

1. Superposition principle:

2. Green’s function:

where

Equation for quasi-steady-state flow period:

Methods of analysis and parameters being estimated

Analysis is based either on the superposition principle or on Green’s function.

1) use initial recovery data for straight line (the transmissivity value calculated using Green’s function would be twice lower).

Applying superposition principle gives:

Applying Green’s function gives:

Unsteady-state flow equations

1. Superposition principle:

2. Green’s function:

where

Steady-state flow equations

1. Superposition principle:

where

2. Green’s function:

where

Methods of analysis and parameters being estimated

Analysis is based either on the superposition principle or on Green’s function.

1) use final recovery data for straight line (the transmissivity value calculated using Green’s function would be twice lower).

2) the graph is plotted only for the equation based on superposition principle.

Unsteady-state flow equations

1. Superposition principle:

2. Green’s function:

where

Methods of analysis and parameters being estimated

Analysis is based either on the superposition principle or on Green’s function.

1) use steady-state (the transmissivity value calculated using Green’s function would be twice lower).

2) for drawdown only; the graph is plotted only for the equation based on superposition principle.

Applying superposition principle gives:

Applying Green’s function gives: