Aquifer of infinite lateral extent (Theis’s method)
Assumptions:
✓aquifer is confined, isotropic, of infinite lateral extent;
✓drawdown in the aquifer could be calculated at any distance from the pumping well;
✓drawdown develops in two stages: unsteady-state flow and quasi-steady-state flow;
✓storage capacity of the pumping well as well as skin effect and storage capacity of the observation well could be taken into account (see corresponding complimentary solutions below).
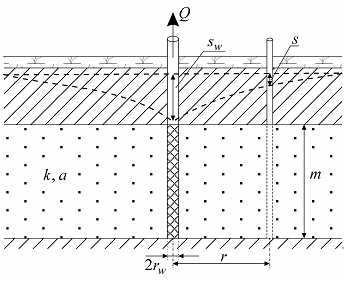
Confined aquifer of lateral infinite extent (cross section).
Fundumental equation:
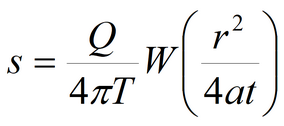
Laplace transform solution:
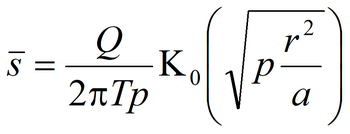
Besides the fundamental equation the following complementary solutions are applied:
1) Moench’s solution for drawdown in the fully penetrating observation well in confined aquifer; the solution takes into account storage capacity of the pumping well, storage capacity of the observation well and skin effect of the pumping well.
Code of WTAQ3 program is used for calculation (author Moench, 1997). See:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
2) Moench’s solution for drawdown in the pumping well in confined aquifer; the solution takes into account the storage capacity and the skin effect of the pumping well.
Code of WTAQ3 program is used for calculation (author Moench, 1997). See:
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
3) Popadopulos’s solution for drawdown in the fully penetrating observation well in confined aquifer; storage capacity of the pumping well is taken into account
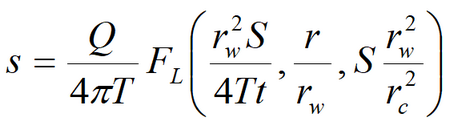
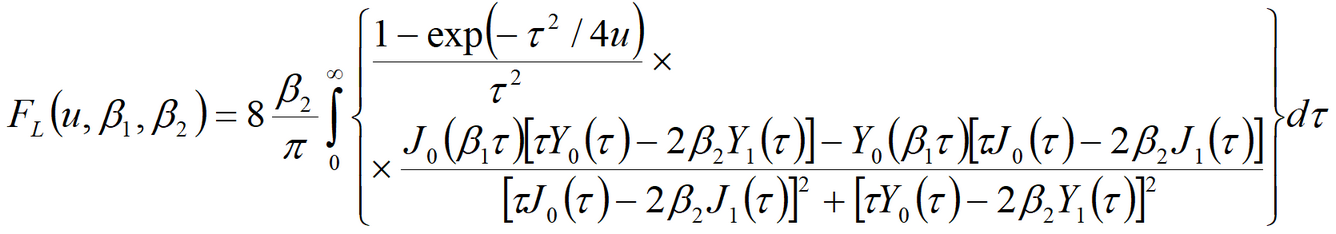
Laplace transform solution:
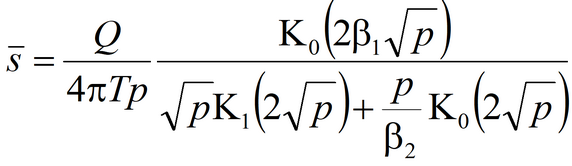
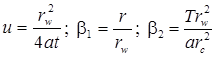
4) Popadopulos’s solution for drawdown in the pumping well in confined aquifer; storage capacity of the pumping well is taken into account
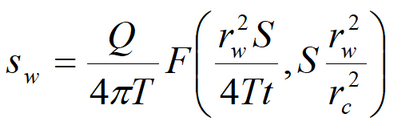
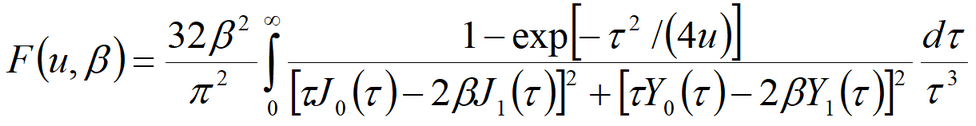
Laplace transform solution:
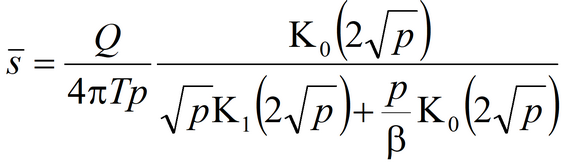
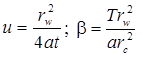
5) Hantush’s solution for the aquifer anisotropic on the lateral plane
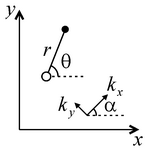
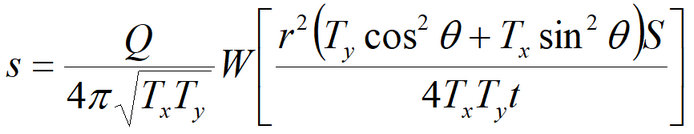
These solutions can be applied in the following cases:
One well pumped at a constant rate
Pumping test
Recovery test
drawdown is counted from the beginning of the pumping test
drawdown is counted from the beginning of the recovery test
The whole test period including pumping /injection/ and recovery stages is analyzed
Several wells pumped at a constant rate
Pumping test (simultaneous start of all pumping wells)
Recovery test after simultaneous start and simultaneous shutdown of all pumping wells
drawdown is counted from the beginning of the pumping test
drawdown is counted from the beginning of the recovery test
The whole test period including pumping /injection/ and recovery stages is analyzed (simultaneous start and simultaneous shutdown of all pumping wells)
Pumping test (asynchronous start of the wells)
One well pumped at a variable rates
Pumping test
Several wells with time-variable pumping rates
Pumping test
Graphical methods are available only for the basic solution. Parameters matching /matching the observed data against theoretical curves/ can also be made using complementary solutions. Then the following additional parameters should be specified such as:
- casing radius of the pumping well,
- skin hydraulic conductivity,
- skin thickness and,
- if needed, shape factor of the observation well.
References
Cooper H.H., Jacob C.E. A generalized graphical method for evaluating formation constants and summarizing well-field history // Transactions, American Geophysical Union. 1946. Vol. 27, N 4. P. 526–534.
Hantush M.S. Analysis of data from pumping tests in anisotropic aquifers // Journal of Geophysical Research. 1966a. Vol. 71, N 2. P. 421–426.
Hantush M.S., Thomas R.G. A method for analyzing a drawdown test in anisotropic aquifers // Water Resources Research. 1966. Vol. 2, N 2. P. 281–285.
Jacob C.E. Effective radius of drawdown test to determine artesian well // Proceedings of the American Society of Civil Engineers. 1946. Vol. 72, N 5. P. 629–646.
Moench A.F. Flow to a well of finite diameter in a homogeneous, anisotropic water table aquifer // Water Resources Research. 1997. Vol. 33, N 6. P. 1397–1407.
Papadopulos I.S., Cooper H.H. Drawdown in a well of large diameter // Water Resources Research. 1967. Vol. 3, N 1. P. 241–244.
Theis C.V. The relation between the lowering of the piezometric surface and the rate and duration of discharge of a well using ground-water storage // Transactions, American Geophysical Union. 1935. Vol. 35, pt. 2. P. 519–524.